feidmath v0.1

Koleksi LAMBDA feidmath v0.1

Penulis

Taruma Sakti Megariansyah

Diterbitkan

Jumat, 26 Mei 2023

Official GIST feidmath (v0.1.x)

https://gist.github.com/taruma/8b0978227dffbee50c3a9d56e31d34f3

feidlambda-math atau feidmath merupakan kumpulan fungsi LAMBDA yang fokus menyelesaikan beberapa permasalahan matematis seperti perkalian matriks, rotasi, interpolasi, dlsbnya. Pengembangan feidmath diusahakan tidak memerlukan fungsi dari feidlambda sehingga fungsi yang tersedia feidmath terisolasi dan dapat digunakan secara langsung sesuai kebutuhan. feidmath dibuat untuk fokus pengembangan yang bersifat penerapan dengan fungsi matematika. feidmath merupakan langkah awal untuk pengembangan koleksi LAMBDA lainnya yang bersifat terapan.

feidmath v0.1 di rilis bersamaan dengan feidlambda v0.4.

Fungsi feidmath v0.1.x

Mengikuti panduan FIAKO LAMBDA Style Guide dan feidlambda v0.4, feidmath dipisahkan dengan kategori yang sesuai dengan fungsi yang tersedia. Berikut kategori yang tersedia di feidmath v0.1.x:

NEW INTERPOLATION_*: Kategori ini berisi fungsi untuk estimasi nilai berdasarkan data yang sudah diketahui.
NEW LINALG_*: Ini mencakup fungsi-fungsi yang berkaitan dengan aljabar linear, seperti operasi pada vektor dan matriks
NEW GEOMETRY_*: Kategori ini melibatkan fungsi geometri, termasuk mengidentifikasi titik berada di dalam/luar poligon.

Download excel demonstrasi RELEASE_feidmath_v0_1_0.xlsx, untuk memudahkan mengeksplorasi fungsi baru di feidmath v0.1.x.

Kategori `INTERPOLATION_*`

NEW v0.1 Kategori INTERPOLATION_* merupakan kumpulan fungsi untuk mengestimasi nilai berdasarkan data yang sudah diketahui. Hubungan antar fungsi di kategori ini bisa dilihat di Gambar 2.1.

%%{ init: { 'theme': 'forest' } }%%

flowchart LR
  NONE ---> _INTERPOLATION_LINEAR
  _INTERPOLATION_LINEAR ---> INTERPOLATION_LINEAR

Gambar 2.1: Grafik dependencies kategori INTERPOLATION_*

Fungsi utama kategori INTERPOLATION_* yaitu INTERPOLATION_LINEAR().

Source Code INTERPOLATION_*

// NONE ---> _INTERPOLATION_LINEAR
_INTERPOLATION_LINEAR = LAMBDA(x, known_ys, known_xs,
    LET(
        known_xs, TOCOL(known_xs),
        known_ys, TOCOL(known_ys),
        nrow, ROWS(known_ys),
        known_table, HSTACK(known_xs, known_ys),
        sorted_table, SORT(known_table, 1),
        sorted_xs, CHOOSECOLS(sorted_table, 1),
        sorted_ys, CHOOSECOLS(sorted_table, 2),
        nearest_x, IFS(
            x > MAX(sorted_xs),
            XMATCH(x, sorted_xs, -1),
            x < MIN(sorted_xs),
            XMATCH(x, sorted_xs, 1),
            TRUE,
            XMATCH(x, sorted_xs, -1)
        ),
        index_ys, IF(
            nearest_x < nrow,
            VSTACK(nearest_x, nearest_x + 1),
            VSTACK(nearest_x - 1, nearest_x)
        ),
        select_ys, CHOOSEROWS(sorted_ys, index_ys),
        select_xs, CHOOSEROWS(sorted_xs, index_ys),
        FORECAST.LINEAR(x, select_ys, select_xs)
    )
);

// _INTERPOLATION_LINEAR ---> INTERPOLATION_LINEAR
INTERPOLATION_LINEAR = LAMBDA(x_vector, known_ys, known_xs,
    LET(
        x_vector, TOCOL(x_vector),
        y_vector, BYROW(
            x_vector,
            LAMBDA(x, _INTERPOLATION_LINEAR(x, known_ys, known_xs))
        ),
        y_vector
    )
);

`INTERPOLATION_LINEAR()`

Fungsi INTERPOLATION_LINEAR(x_vector, known_y, known_x) digunakan untuk mencari nilai interpolasi linear. Fungsi ini dikembangkan menggunakan fungsi bawaan FORECAST.LINEAR(...). Fungsi ini bisa menerima input scalar maupun vector.

Syntax: INTERPOLATION_LINEAR(x_vector, known_y, known_x)
Output: scalar / vector

x_vector := [scalar | vector]: Poin data yang ingin Anda prediksikan nilainya.
known_ys := [vector]: vector atau rentang data terikat.
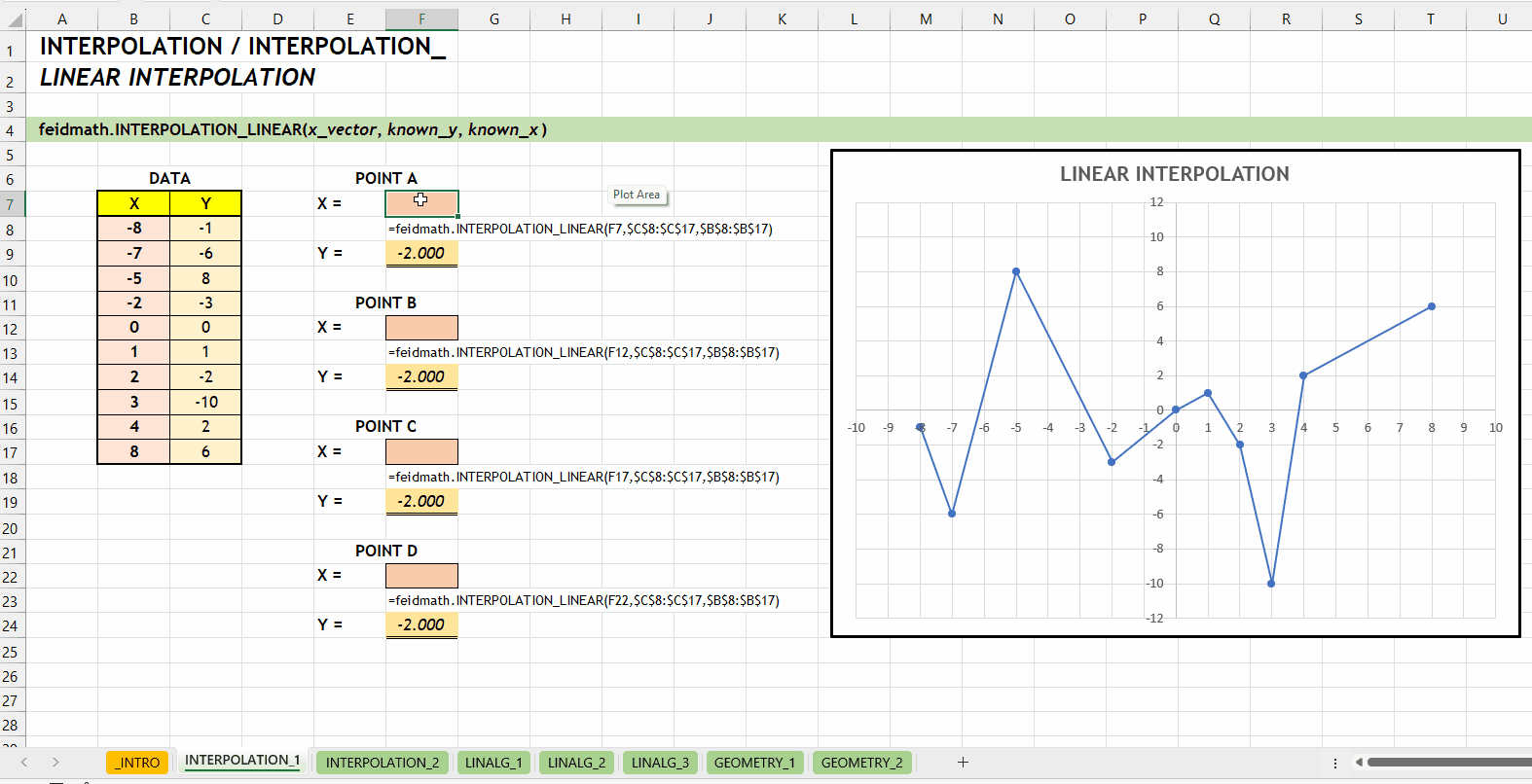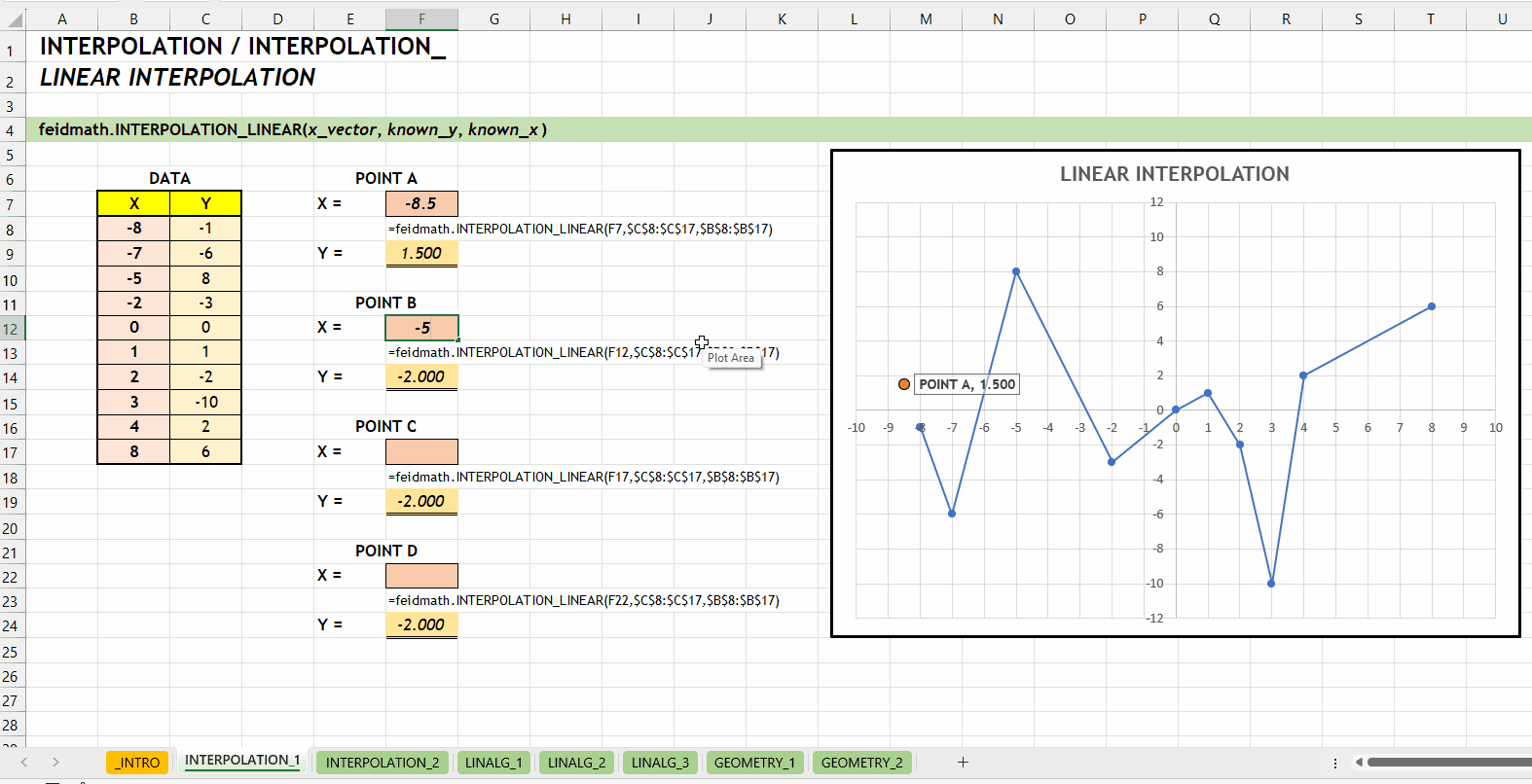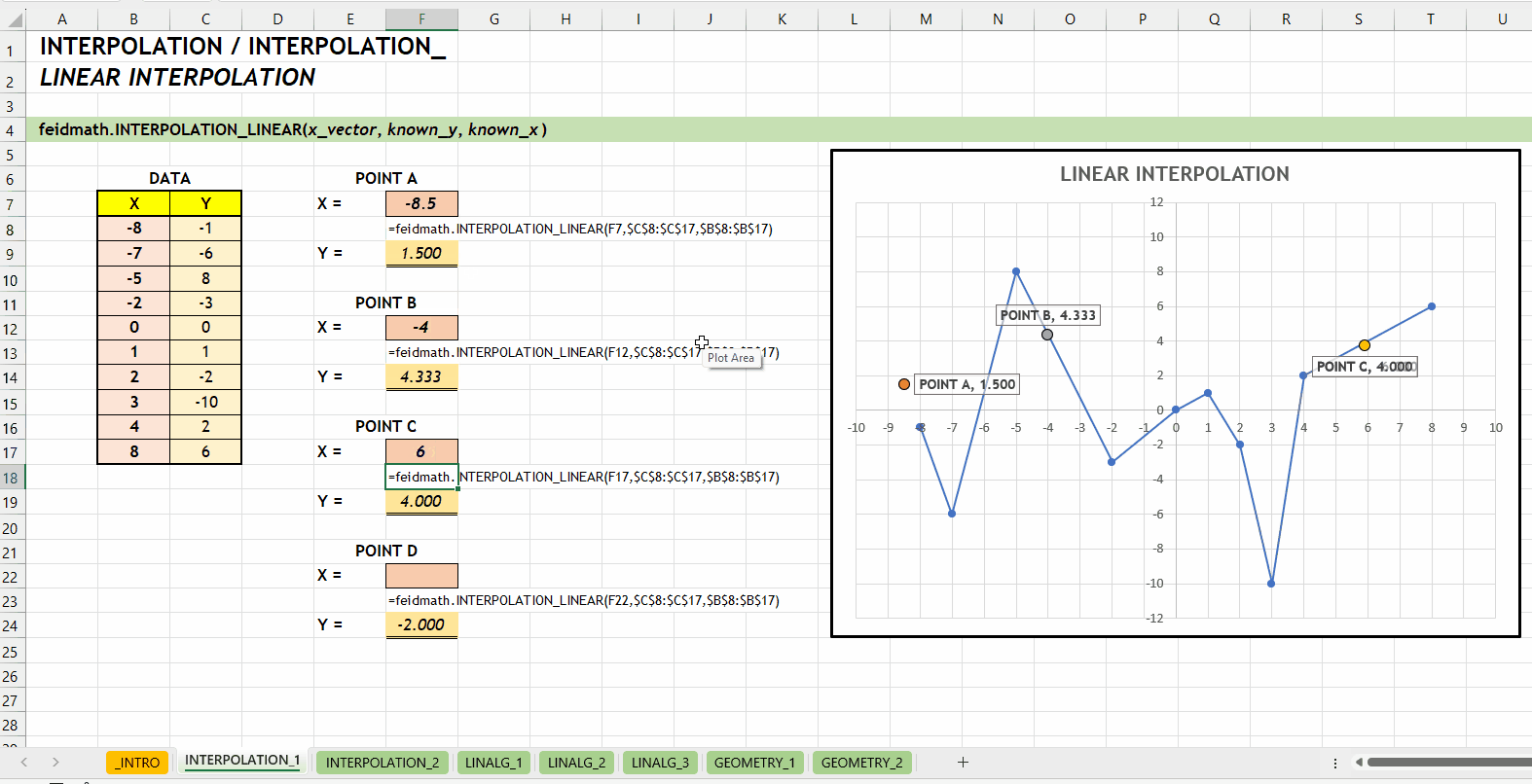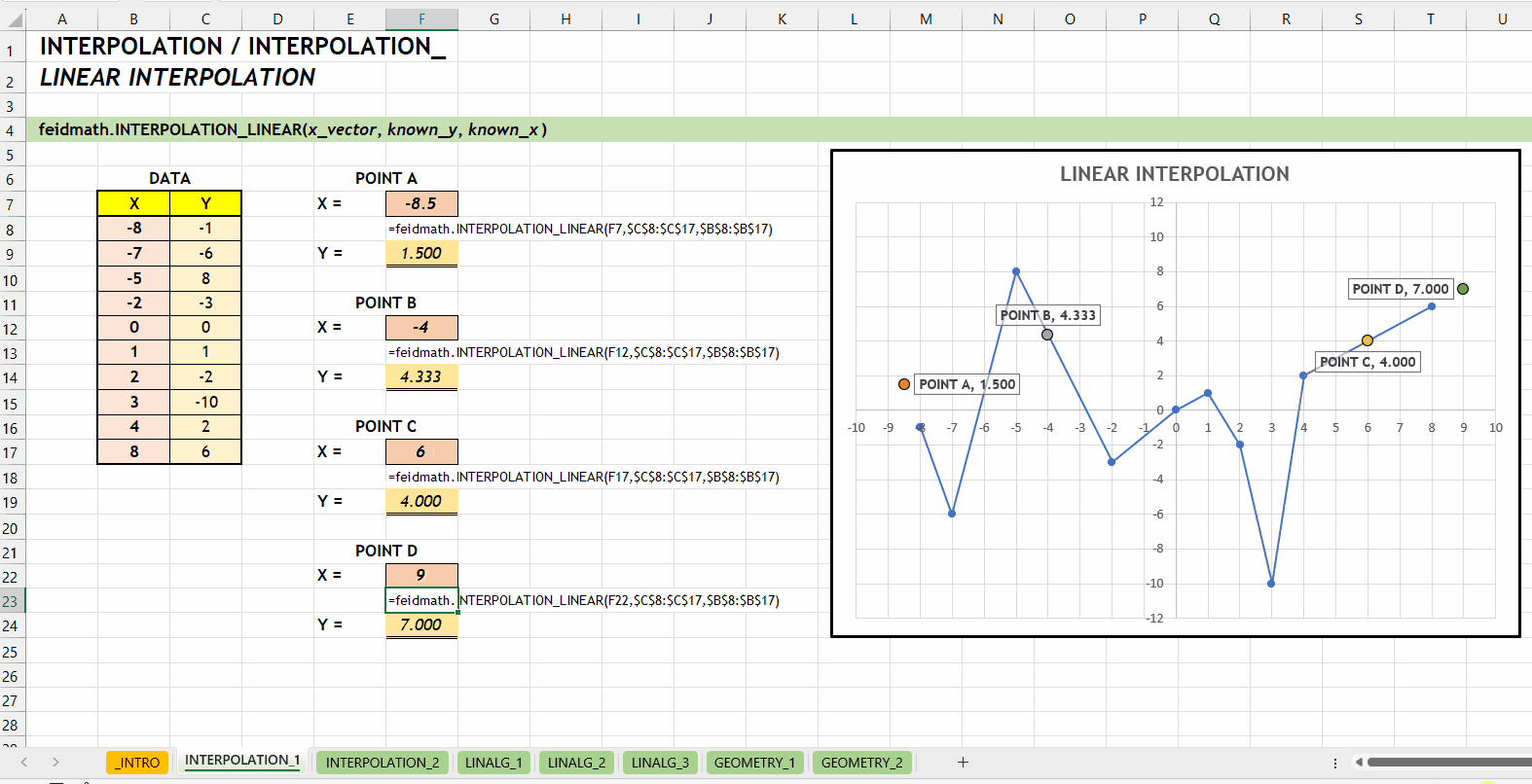
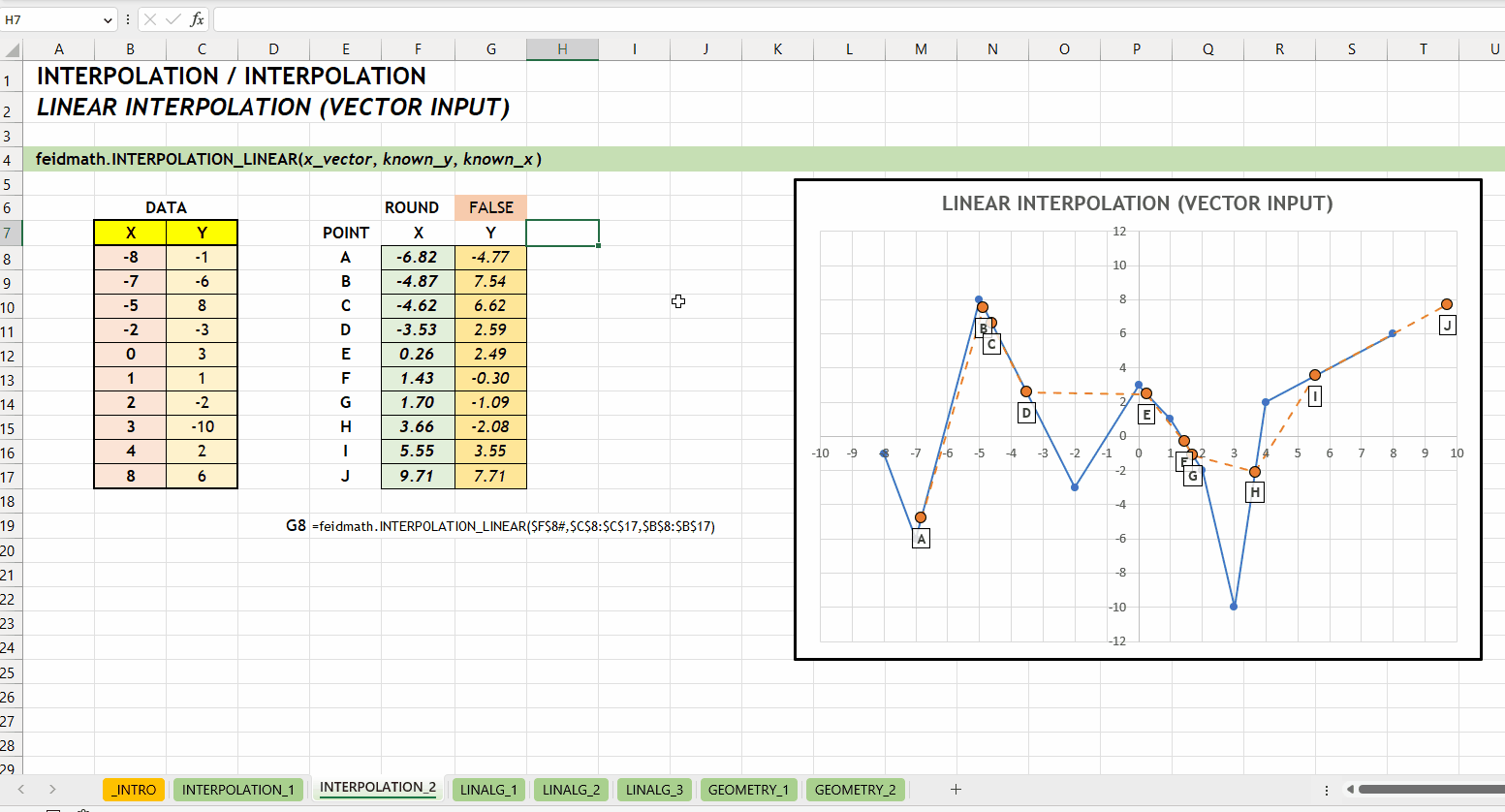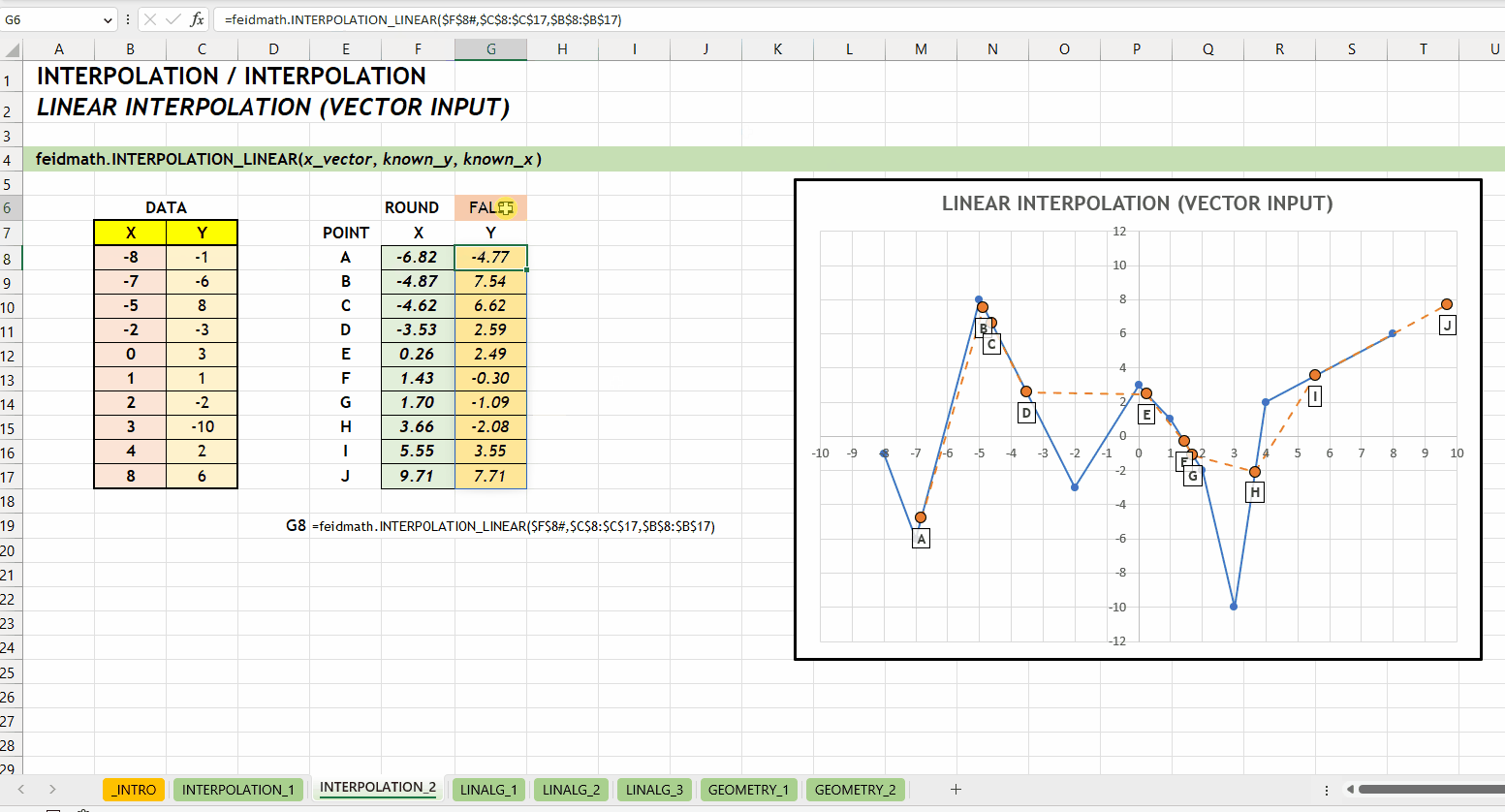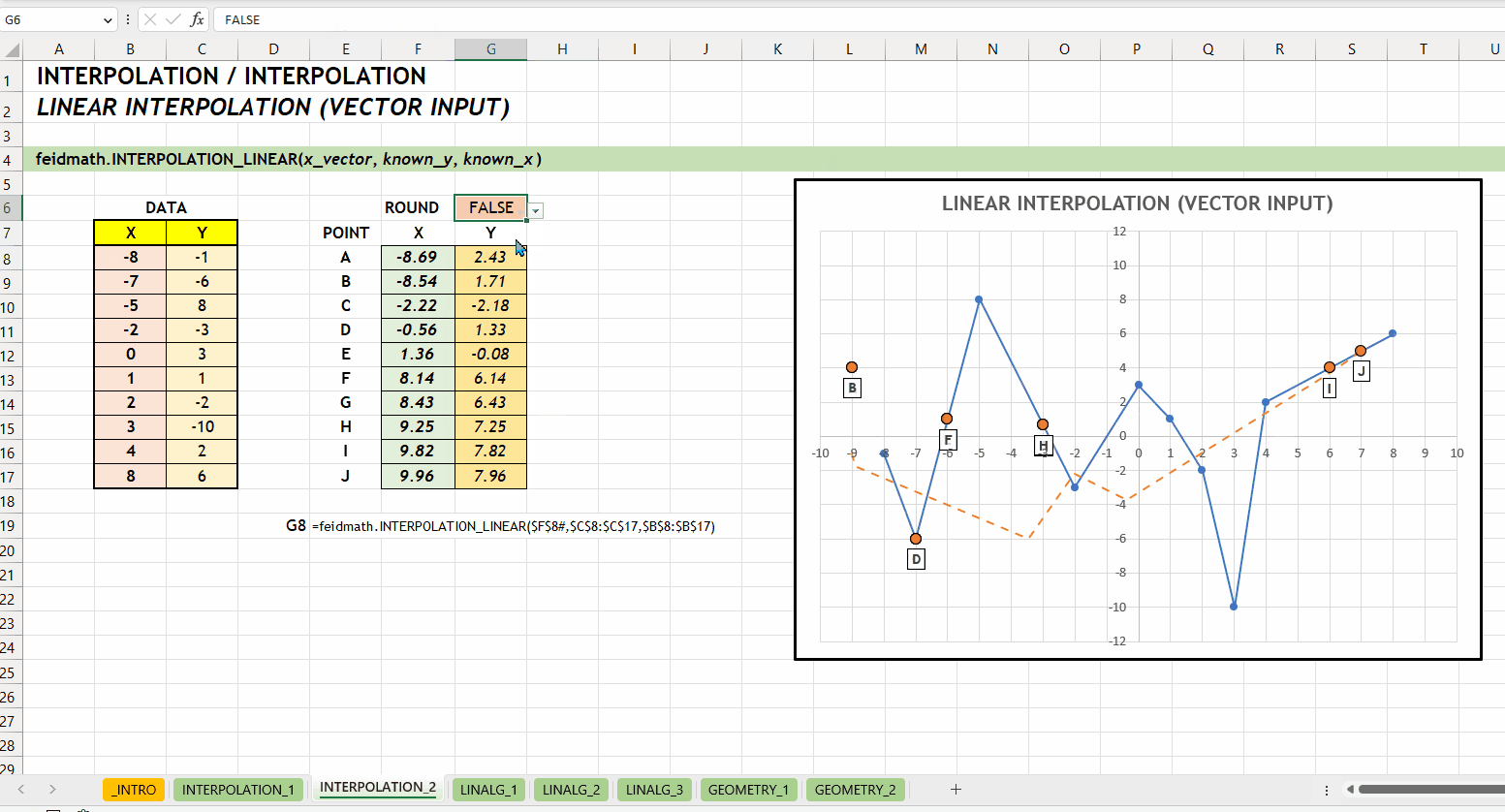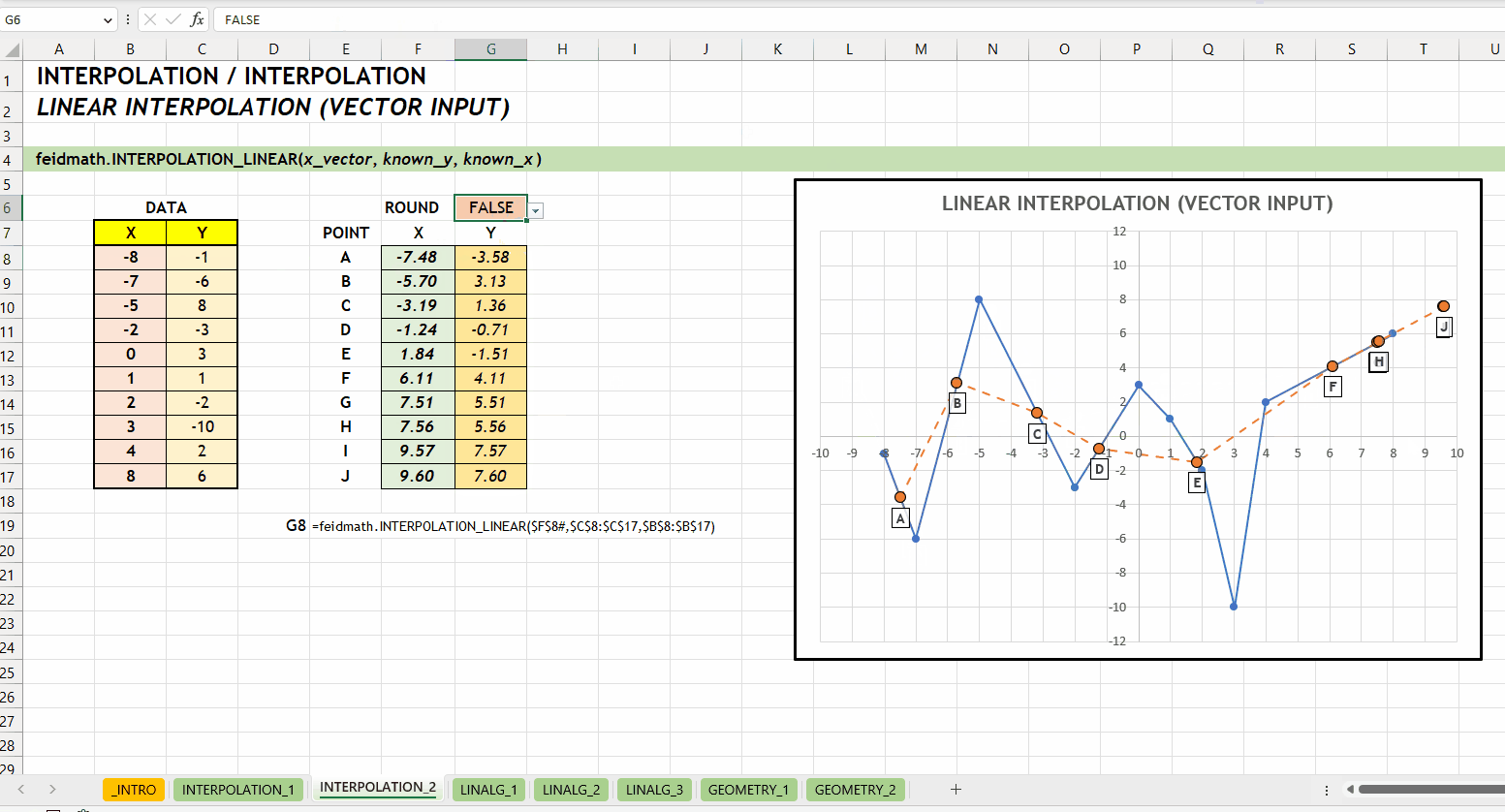
known_xs := [vector]: vector atau rentang data terikat.

Kategori `LINALG_*`

NEW v0.1 Kategori LINALG_* merupakan kumpulan fungsi yang berkaitan dengan aljabar linear seperti operasi pada vektor atau matriks. LINALG merupakan singkatan dari LINEAR ALGEBRA. Hubungan antar fungsi di kategori ini bisa dilihat di Gambar 3.1.

%%{ init: { 'theme': 'forest' } }%%

flowchart LR
  NONE ---> LINALG_ROTATION_MATRIX
  LINALG_ROTATION_MATRIX ---> LINALG_ROTATE_POINT
  LINALG_ROTATE_POINT ---> _RECURSIVE_ROTATE_POINTS
  _RECURSIVE_ROTATE_POINTS ---> _RECURSIVE_ROTATE_POINTS
  _RECURSIVE_ROTATE_POINTS ---> LINALG_ROTATE_POINT_ARRAY

Gambar 3.1: Grafik dependencies kategori LINALG_*

Fungsi utama kategori LINALG_* yaitu LINALG_ROTATION_MATRIX(), LINALG_ROTATE_POINT(), dan LINALG_ROTATE_POINT_ARRAY().

Source Code LINALG_*

// NONE ---> LINALG_ROTATION_MATRIX
LINALG_ROTATION_MATRIX = LAMBDA(theta_x, theta_y, theta_z, [num_digits],
    LET(
        round_number, IF(ISOMITTED(num_digits), 0, num_digits),
        angle_x, RADIANS(theta_x),
        angle_y, RADIANS(theta_y),
        angle_z, RADIANS(theta_z),
        cos_x, COS(angle_x),
        sin_x, SIN(angle_x),
        rotation_x, VSTACK(
            HSTACK(1, 0, 0),
            HSTACK(0, cos_x, -sin_x),
            HSTACK(0, sin_x, cos_x)
        ),
        cos_y, COS(angle_y),
        sin_y, SIN(angle_y),
        rotation_y, VSTACK(
            HSTACK(cos_y, 0, sin_y),
            HSTACK(0, 1, 0),
            HSTACK(-sin_y, 0, cos_y)
        ),
        cos_z, COS(angle_z),
        sin_z, SIN(angle_z),
        rotation_z, VSTACK(
            HSTACK(cos_z, -sin_z, 0),
            HSTACK(sin_z, cos_z, 0),
            HSTACK(0, 0, 1)
        ),
        rotation_matrix, MMULT(rotation_z, MMULT(rotation_y, rotation_x)),
        IF(
            round_number,
            ROUND(rotation_matrix, round_number),
            rotation_matrix
        )
    )
);

// LINALG_ROTATION_MATRIX ---> LINALG_ROTATE_POINT
LINALG_ROTATE_POINT = LAMBDA(
    point_vector,
    theta_x,
    theta_y,
    theta_z,
    [active_rotation],
    [num_digits],
    LET(
        active_rotation, IF(
            ISOMITTED(active_rotation),
            TRUE,
            active_rotation
        ),
        rotation_matrix, LINALG_ROTATION_MATRIX(
            theta_x,
            theta_y,
            theta_z,
            num_digits
        ),
        point_vector, TOCOL(point_vector),
        final_rotation, IF(
            active_rotation,
            rotation_matrix,
            TRANSPOSE(rotation_matrix)
        ),
        point_rotation, MMULT(final_rotation, point_vector),
        TOROW(point_rotation)
    )
);

// LINALG_ROTATE_POINT ---> _RECURSIVE_ROTATE_POINTS
// _RECURSIVE_ROTATE_POINTS ---> _RECURSIVE_ROTATE_POINTS
_RECURSIVE_ROTATE_POINTS = LAMBDA(
    ntry,
    data_points,
    theta_x,
    theta_y,
    theta_z,
    [active_rotation],
    [num_digits],
    LET(
        selected_row, CHOOSEROWS(data_points, ntry),
        IF(
            ntry = 1,
            LINALG_ROTATE_POINT(
                selected_row,
                theta_x,
                theta_y,
                theta_z,
                active_rotation,
                num_digits
            ),
            LET(
                next_try, ntry - 1,
                result, LINALG_ROTATE_POINT(
                    selected_row,
                    theta_x,
                    theta_y,
                    theta_z,
                    active_rotation,
                    num_digits
                ),
                VSTACK(
                    _RECURSIVE_ROTATE_POINTS(
                        next_try,
                        data_points,
                        theta_x,
                        theta_y,
                        theta_z,
                        active_rotation,
                        num_digits
                    ),
                    result
                )
            )
        )
    )
);

// _RECURSIVE_ROTATE_POINTS ---> LINALG_ROTATE_POINT_ARRAY
LINALG_ROTATE_POINT_ARRAY = LAMBDA(
    data_points,
    theta_x,
    theta_y,
    theta_z,
    [active_rotation],
    [num_digits],
    _RECURSIVE_ROTATE_POINTS(
        ROWS(data_points),
        data_points,
        theta_x,
        theta_y,
        theta_z,
        active_rotation,
        num_digits
    )
);

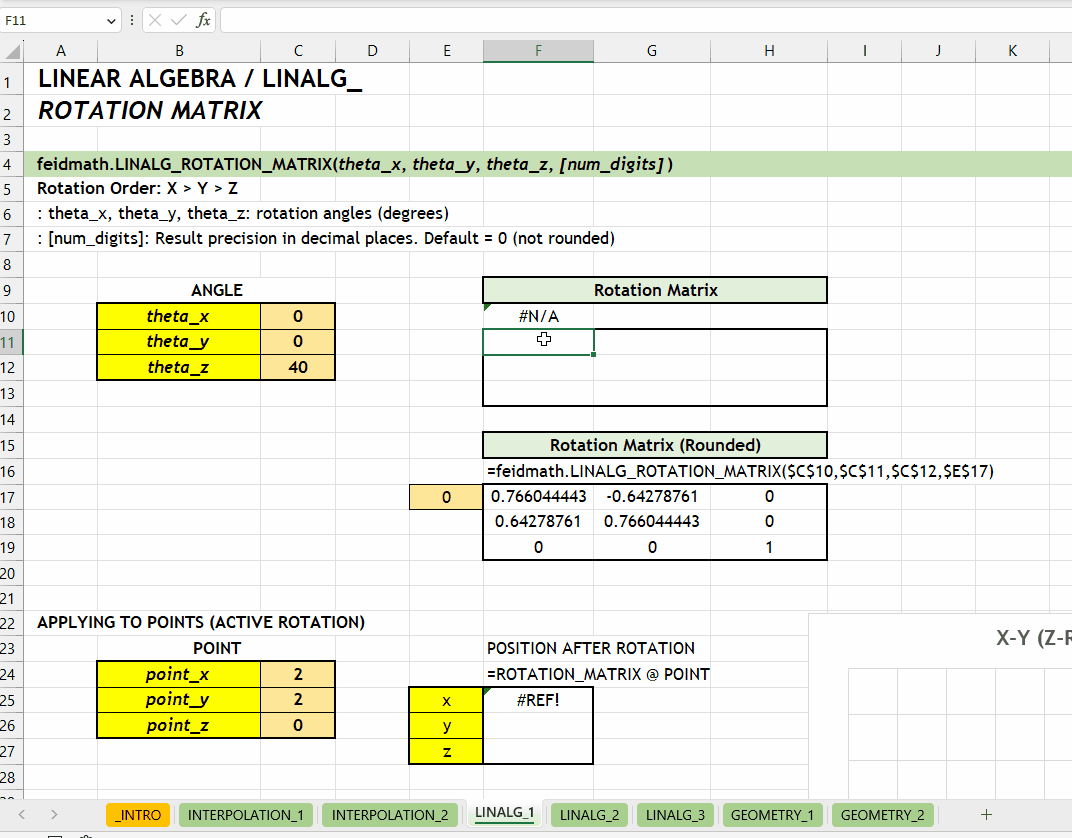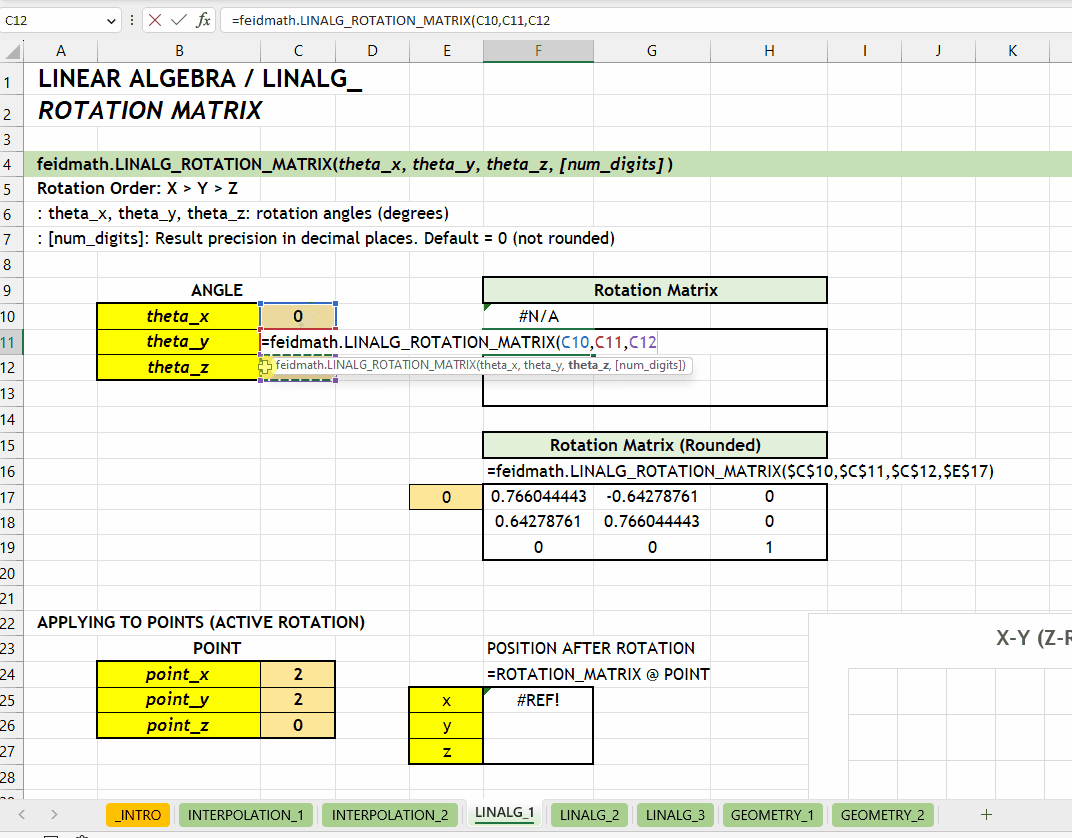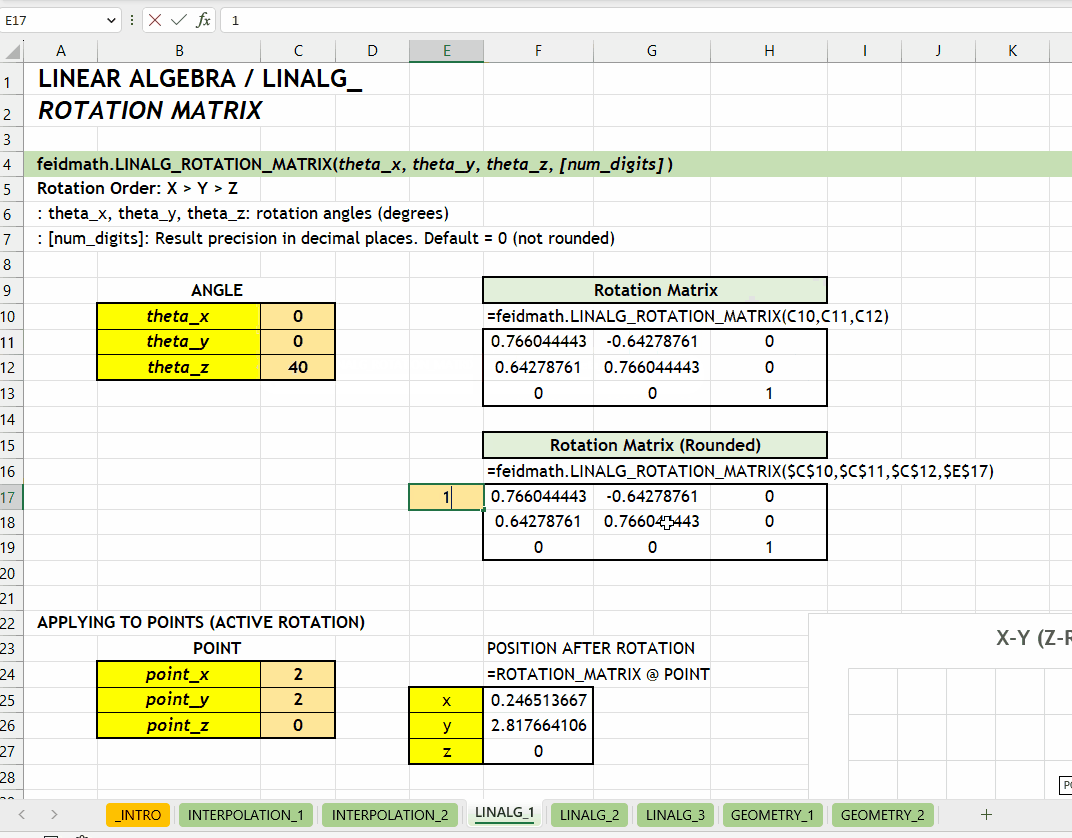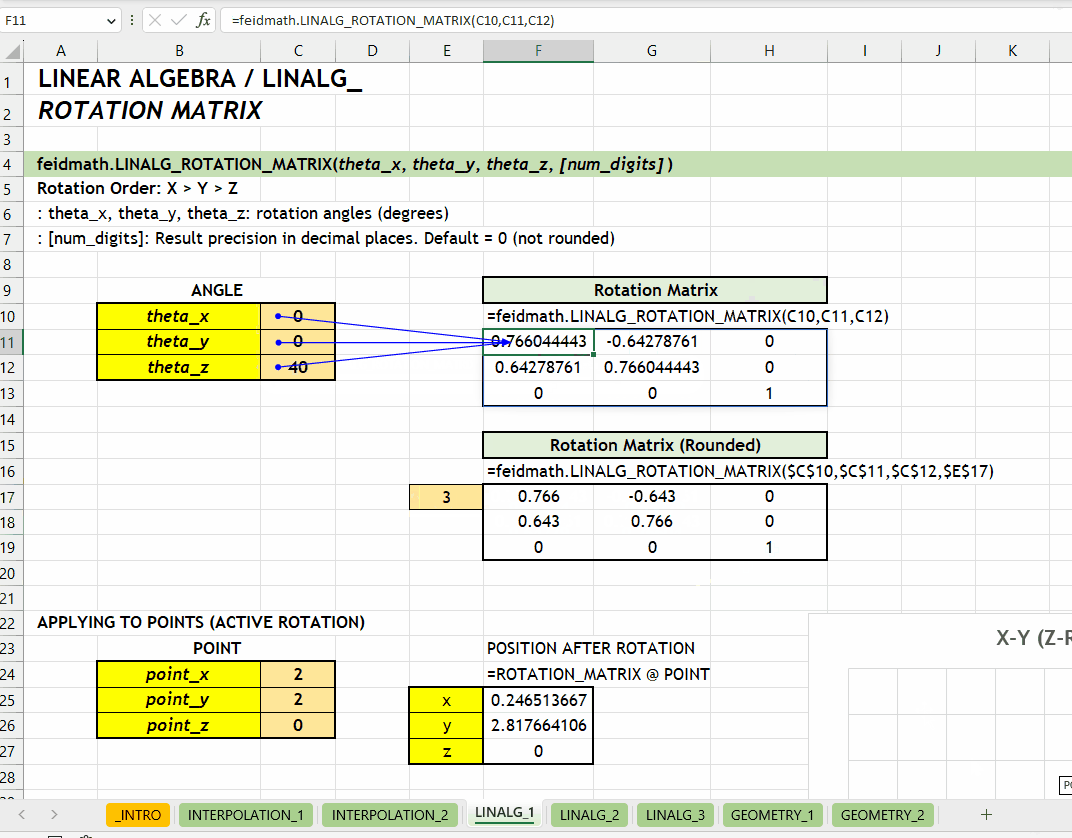
`LINALG_ROTATION_MATRIX()`

Fungsi LINALG_ROTATION_MATRIX(theta_x, theta_y, theta_z, [num_digits]) digunakan untuk menghasilkan matriks rotasi berdasarkan tiga sudut rotasi (\(\theta_x\), \(\theta_y\), dan \(\theta_z\)) yang ditentukan dalam derajat.

Syntax: LINALG_ROTATION_MATRIX(theta_x, theta_y, theta_z, [num_digits])
Output: \(3 \times 3\) array

theta_x | theta_y | theta_z := [number]: Rotasi terhadap sumbu-nya dalam satuan derajat.
[num_digits] := 0 :: [number]: Nilai default yaitu 0 (tidak dibulatkan). Jumlah digit presisi yang diinginkan.

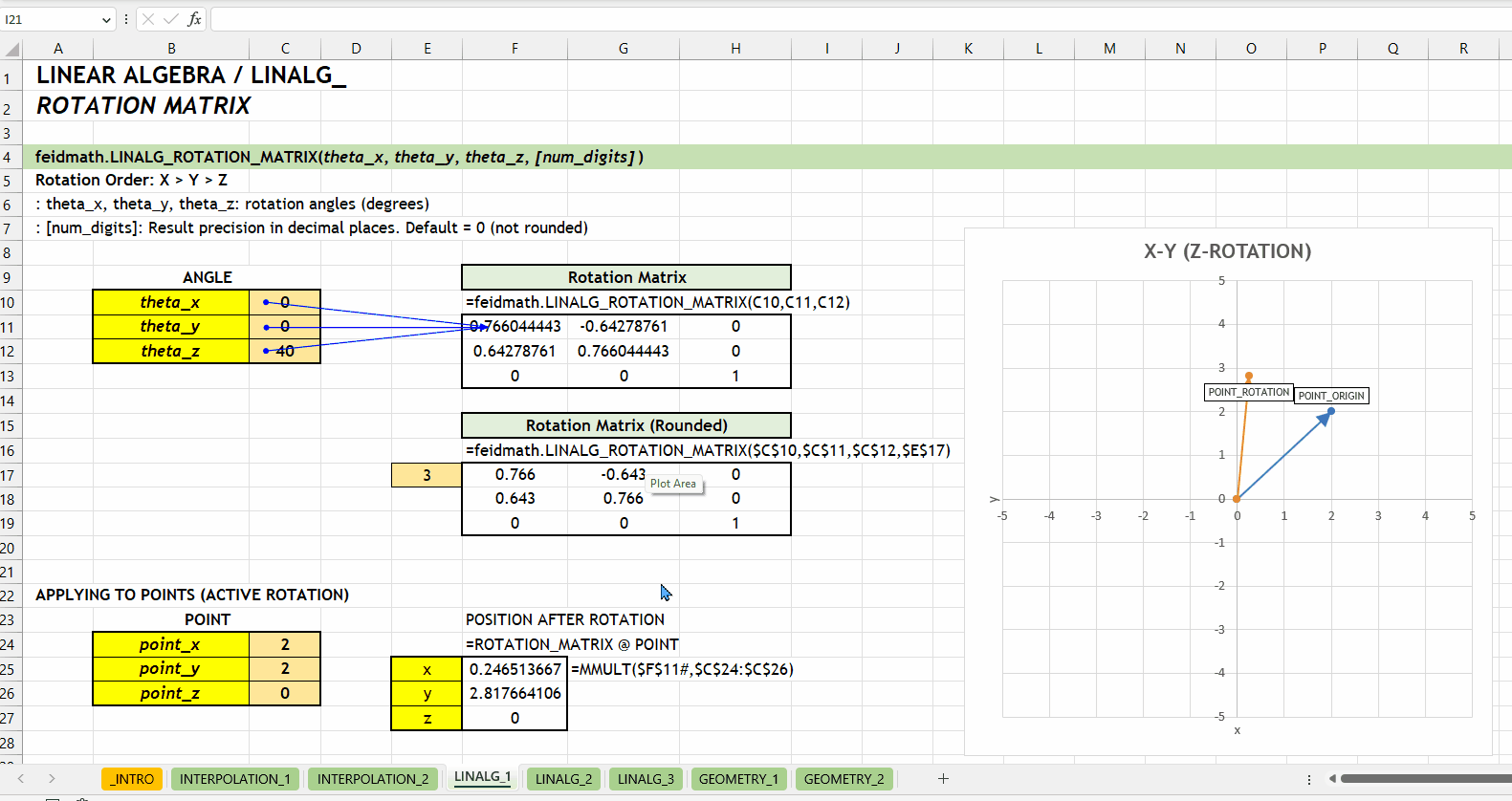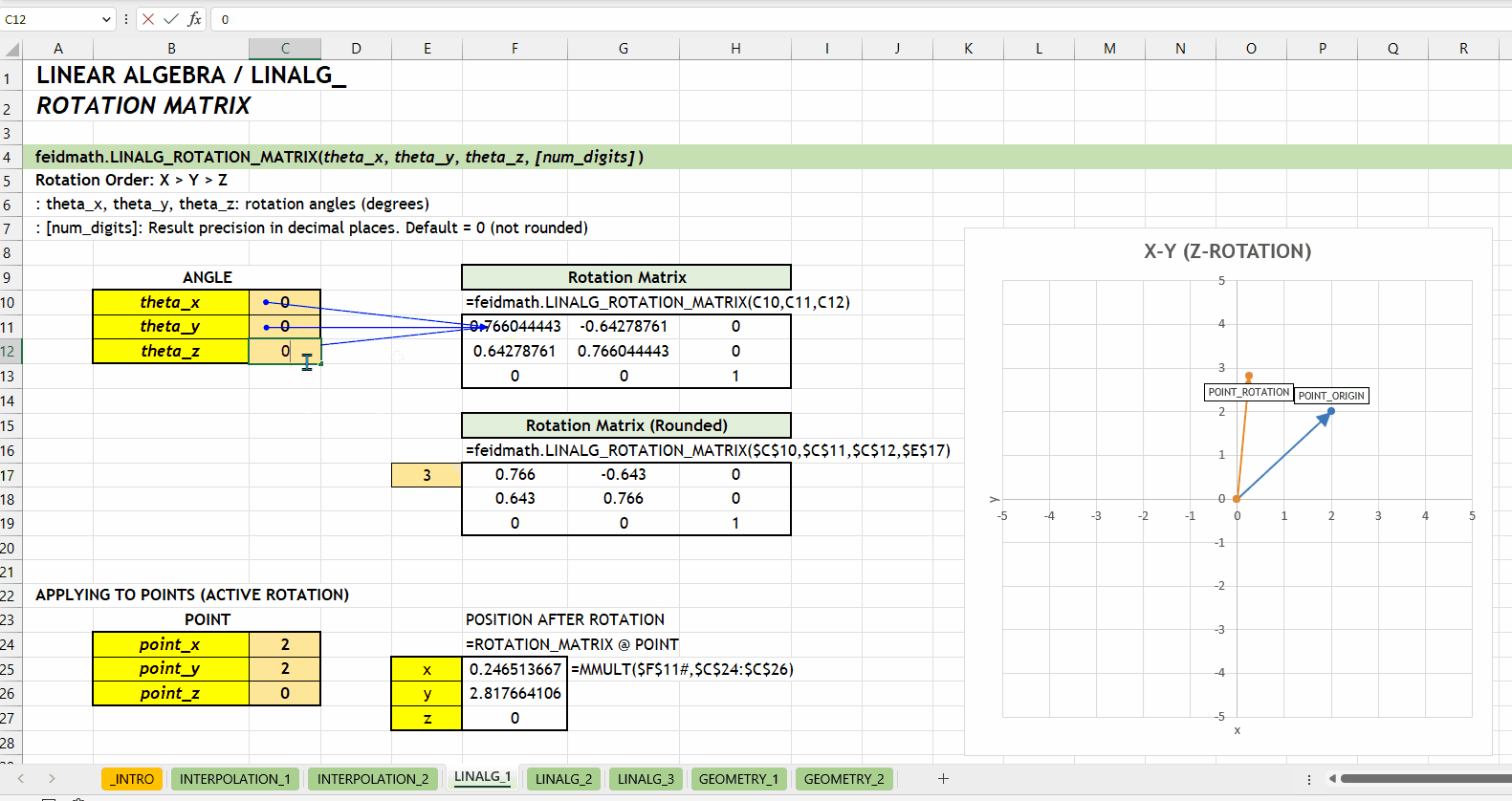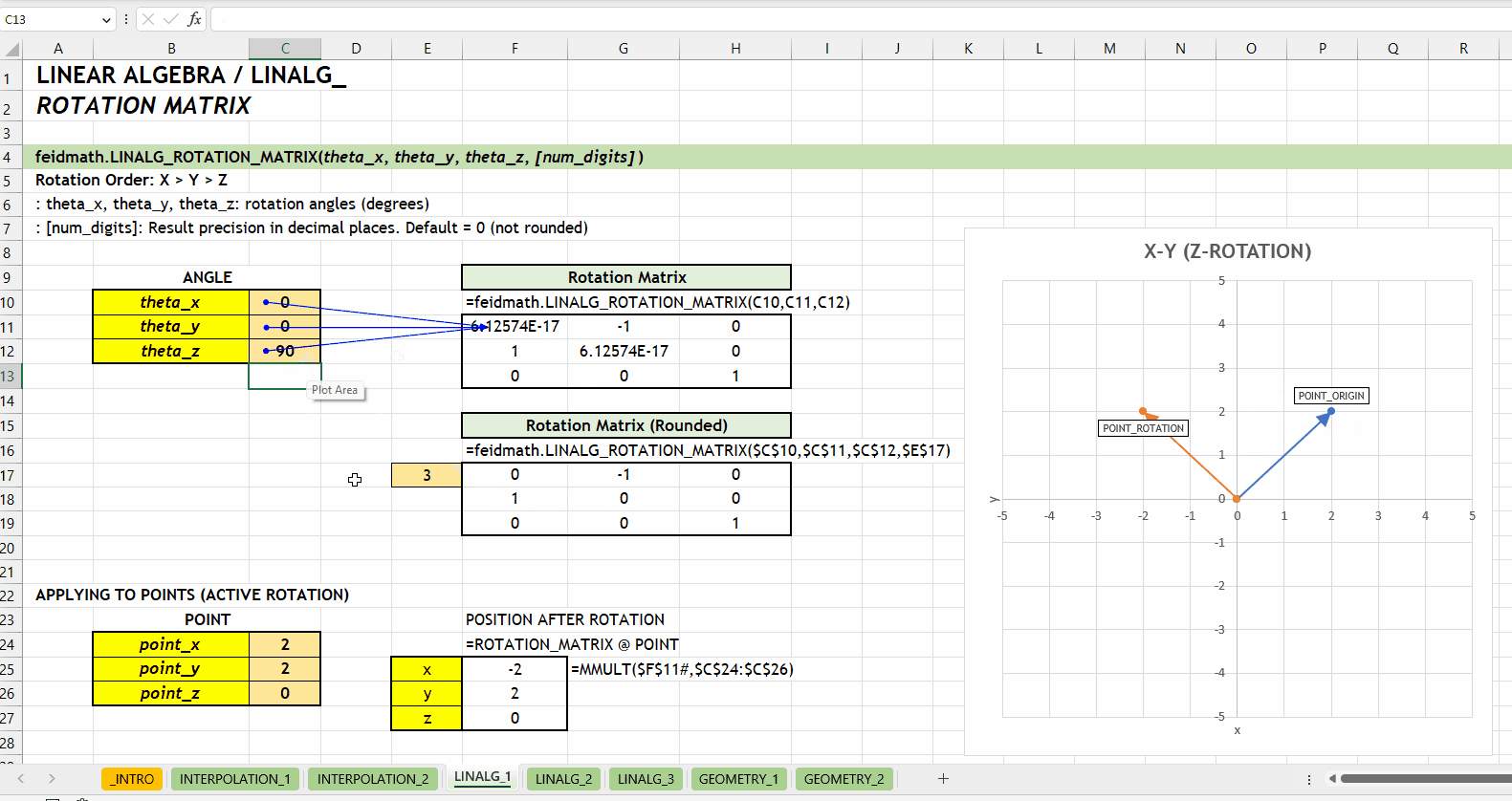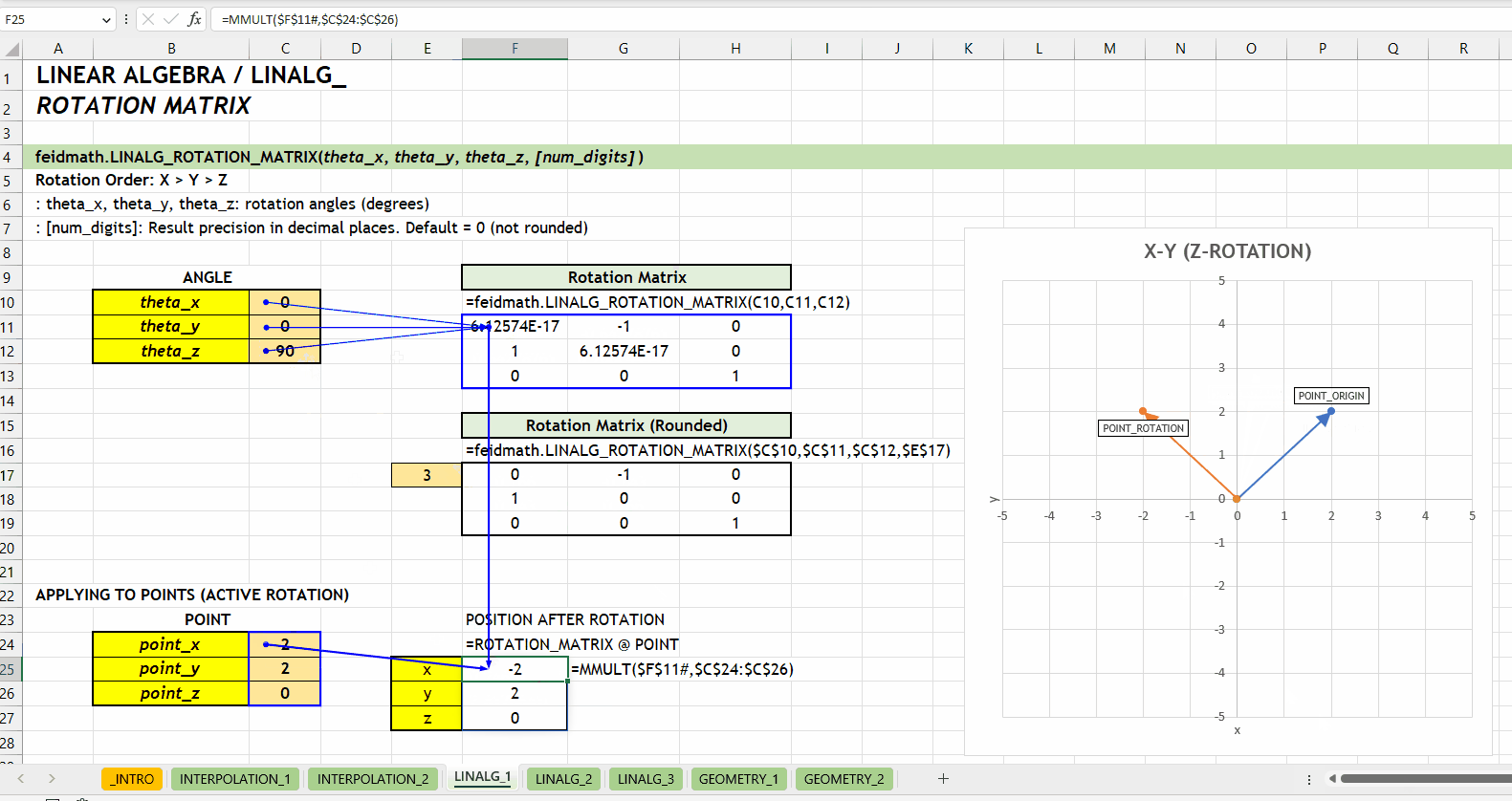
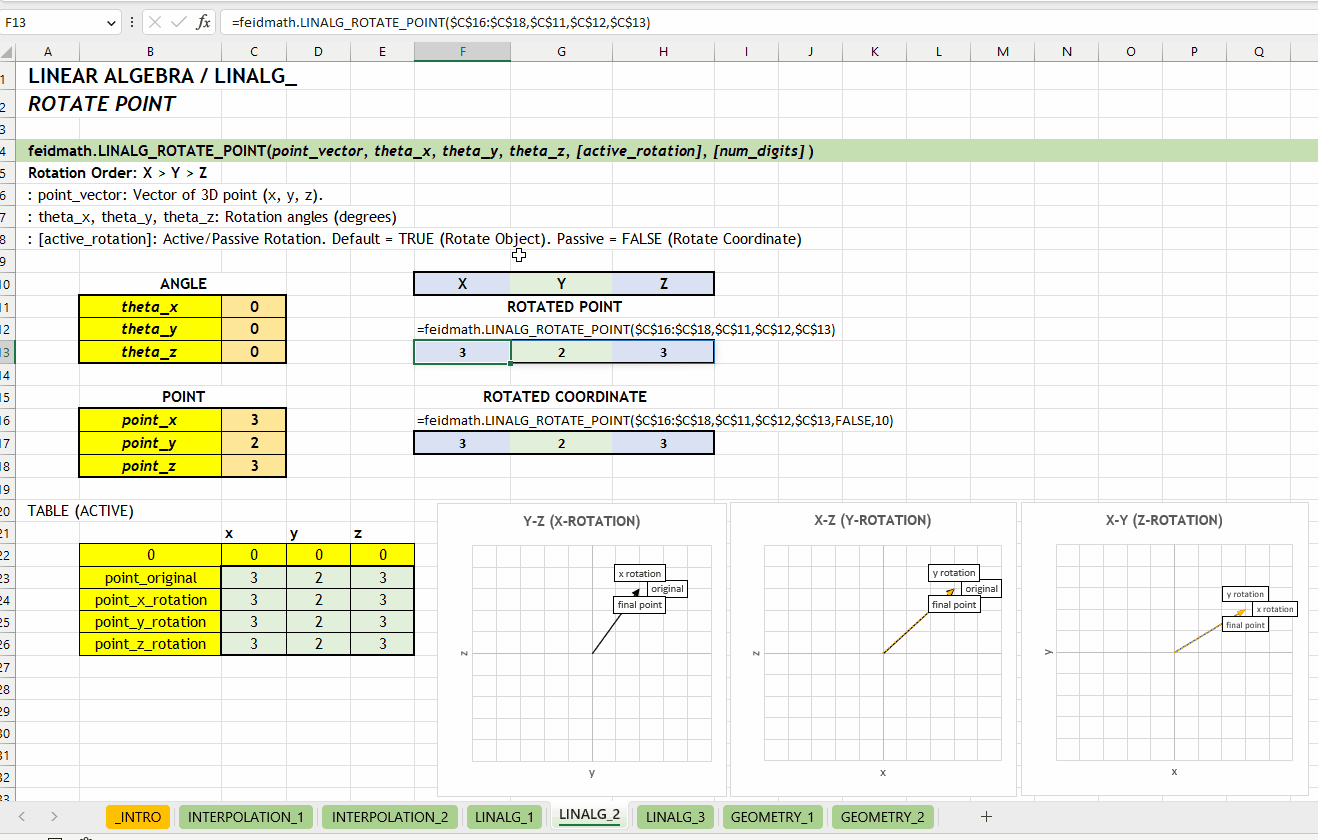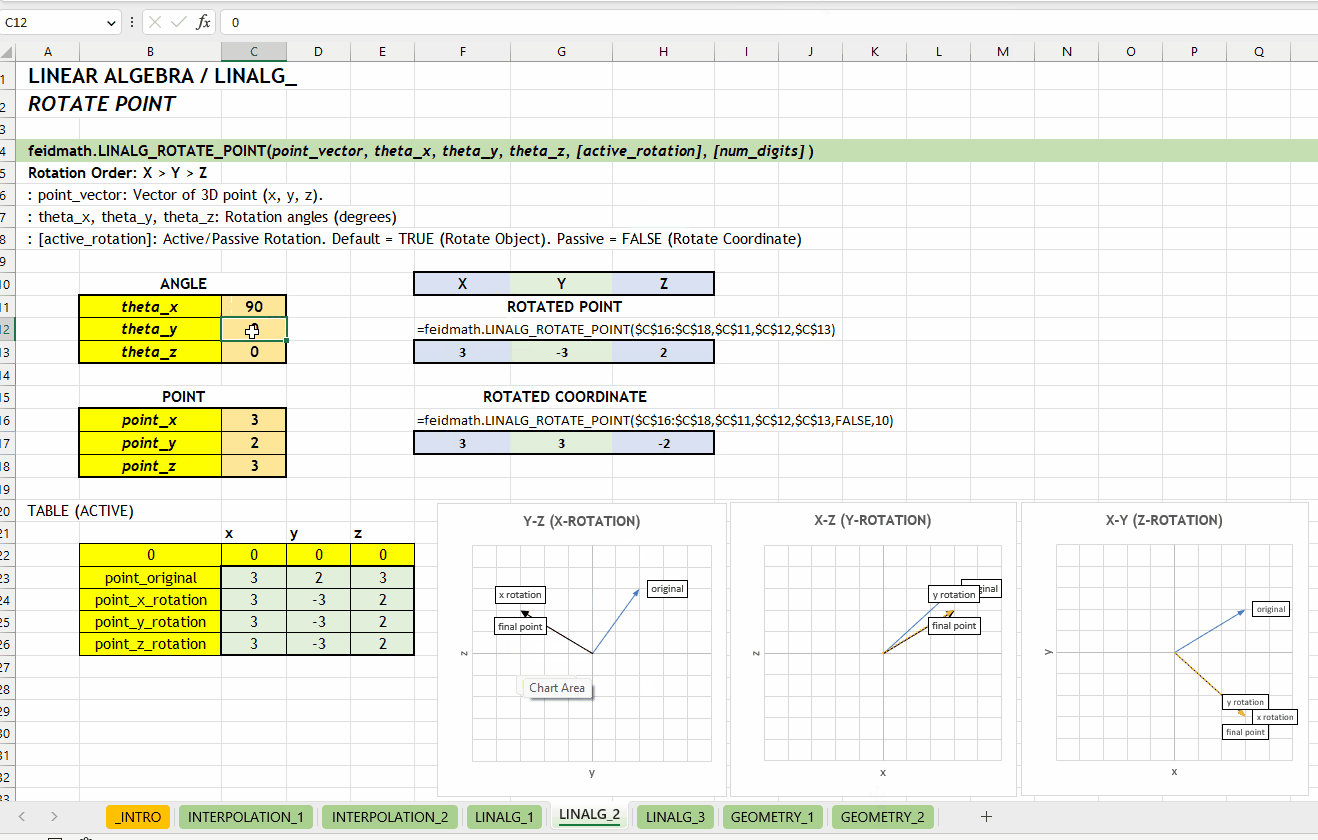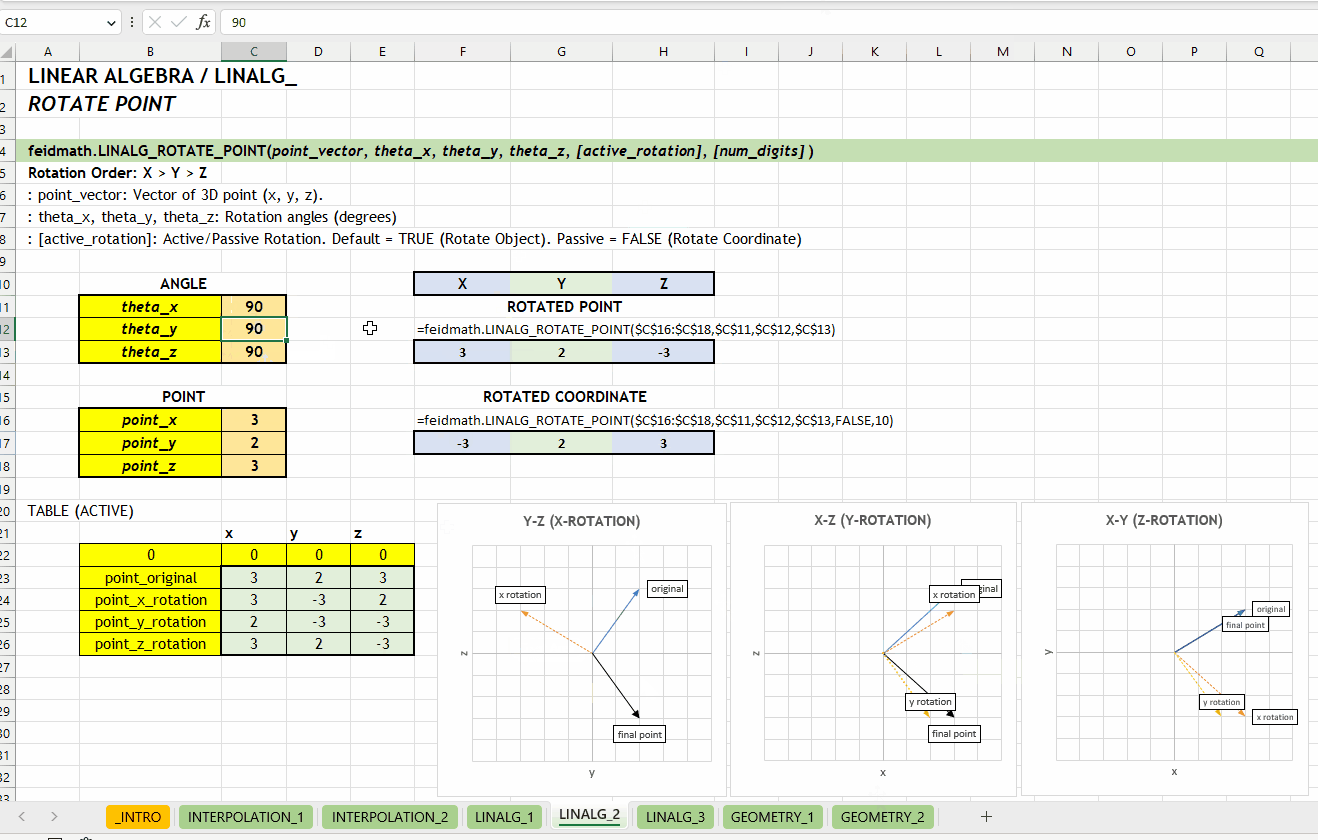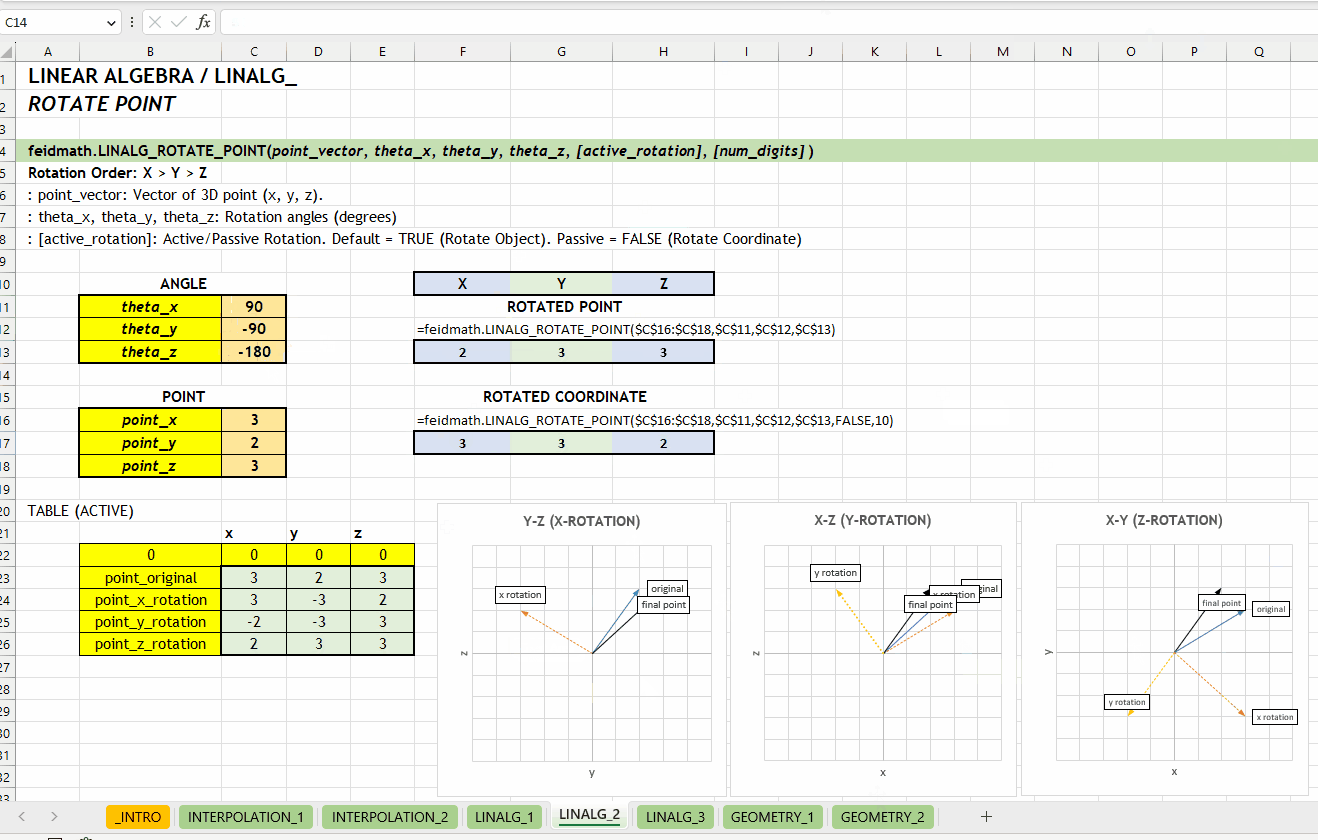
`LINALG_ROTATE_POINT()`

Fungsi LINALG_ROTATE_POINT(point_vector, theta_x, theta_y, theta_z, [active_rotation], [num_digits]) digunakan untuk melakukan rotasi pada titik dalam ruang tiga dimensi. Fungsi ini menerima input dalam bentuk vektor dengan tiga nilai yaitu \(x\), \(y\), dan \(z\).

Syntax: LINALG_ROTATE_POINT(point_vector, theta_x, theta_y, theta_z, [active_rotation], [num_digits])
Output: vector

point_vector := [number vector]: Koordinat titik dalam bentuk vektor (\(x\), \(y\), \(z\)).
theta_x | theta_y | theta_z := [number]: Rotasi terhadap sumbu-nya dalam satuan derajat.
[active_rotation] := TRUE :: [TRUE | FALSE]: Nilai default yaitu TRUE. Rotasi aktif akan mengubah posisi objek, sedangkan rotasi pasif akan mengubah sistem koordinat.
[num_digits] := 0 :: [number]: Nilai default yaitu 0 (tidak dibulatkan). Jumlah digit presisi yang diinginkan.

Gambar 3.3: Demonstrasi `LINALG_ROTATE_POINT()`

`LINALG_ROTATE_POINT_ARRAY()`

Fungsi LINALG_ROTATE_POINT_ARRAY(data_points, theta_x, theta_y, theta_z, [active_rotation], [num_digits]) digunakan untuk melakukan rotasi pada sekumpulan titik dalam ruang tiga dimensi. Fungsi LINALG_ROTATE_POINT_ARRAY() sama dengan LINALG_ROTATE_POINT() tetapi dirancang untuk merotasikan sekumpulan titik sekaligus. Argumen data_points harus berupa array yang setiap barisnya merepresentasikan titik di ruang 3D. Fungsi ini menerima array dengan tiga kolom yaitu \(x\), \(y\), dan \(z\).

Syntax: LINALG_ROTATE_POINT_ARRAY(data_points, theta_x, theta_y, theta_z, [active_rotation], [num_digits])
Output: \(m \times 3\) array

data_points := [number array]: Sekumpulan koordinat titik dalam bentuk array dengan kolom \(x\), \(y\), \(z\).
theta_x | theta_y | theta_z := [number]: Rotasi terhadap sumbu-nya dalam satuan derajat.
[active_rotation] := TRUE :: [TRUE | FALSE]: Nilai default yaitu TRUE. Rotasi aktif akan mengubah posisi objek, sedangkan rotasi pasif akan mengubah sistem koordinat.
[num_digits] := 0 :: [number]: Nilai default yaitu 0 (tidak dibulatkan). Jumlah digit presisi yang diinginkan.

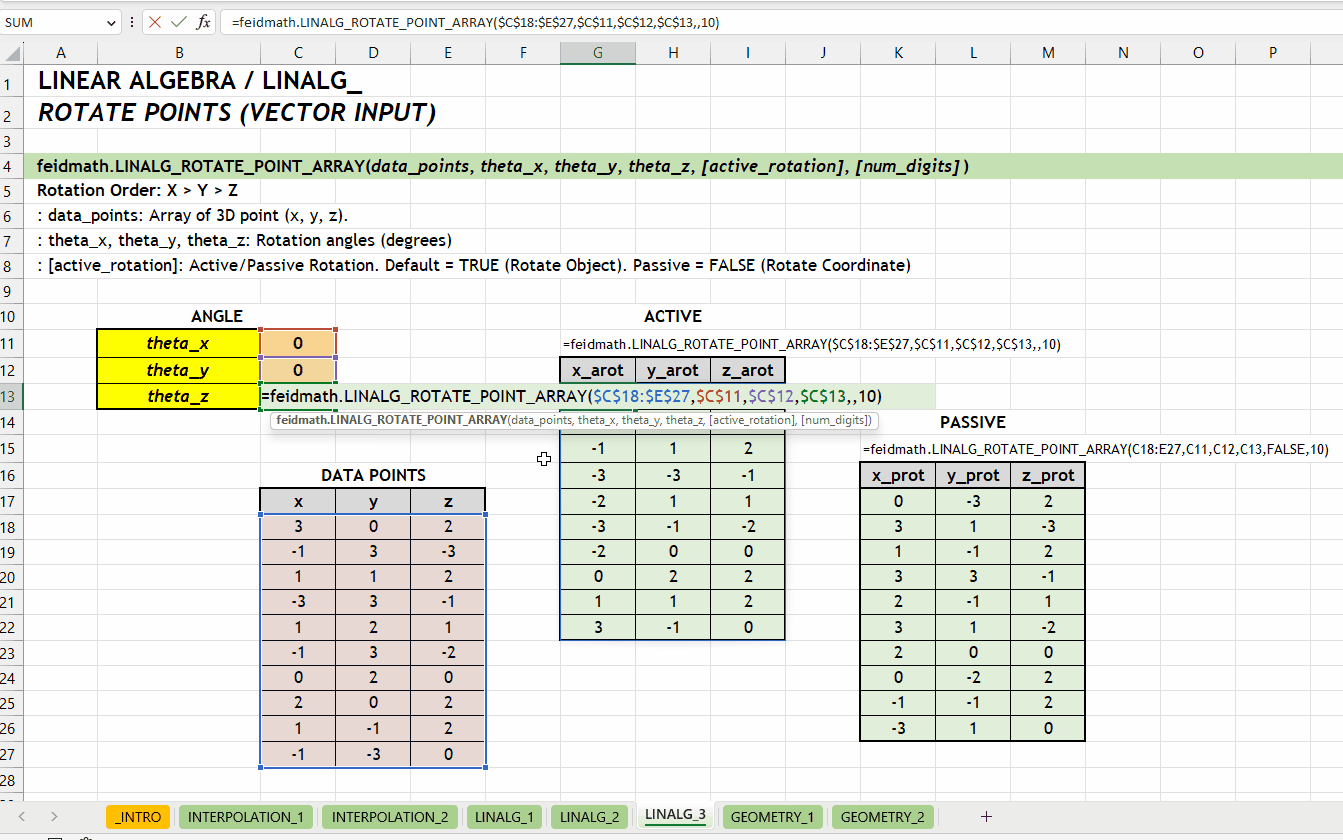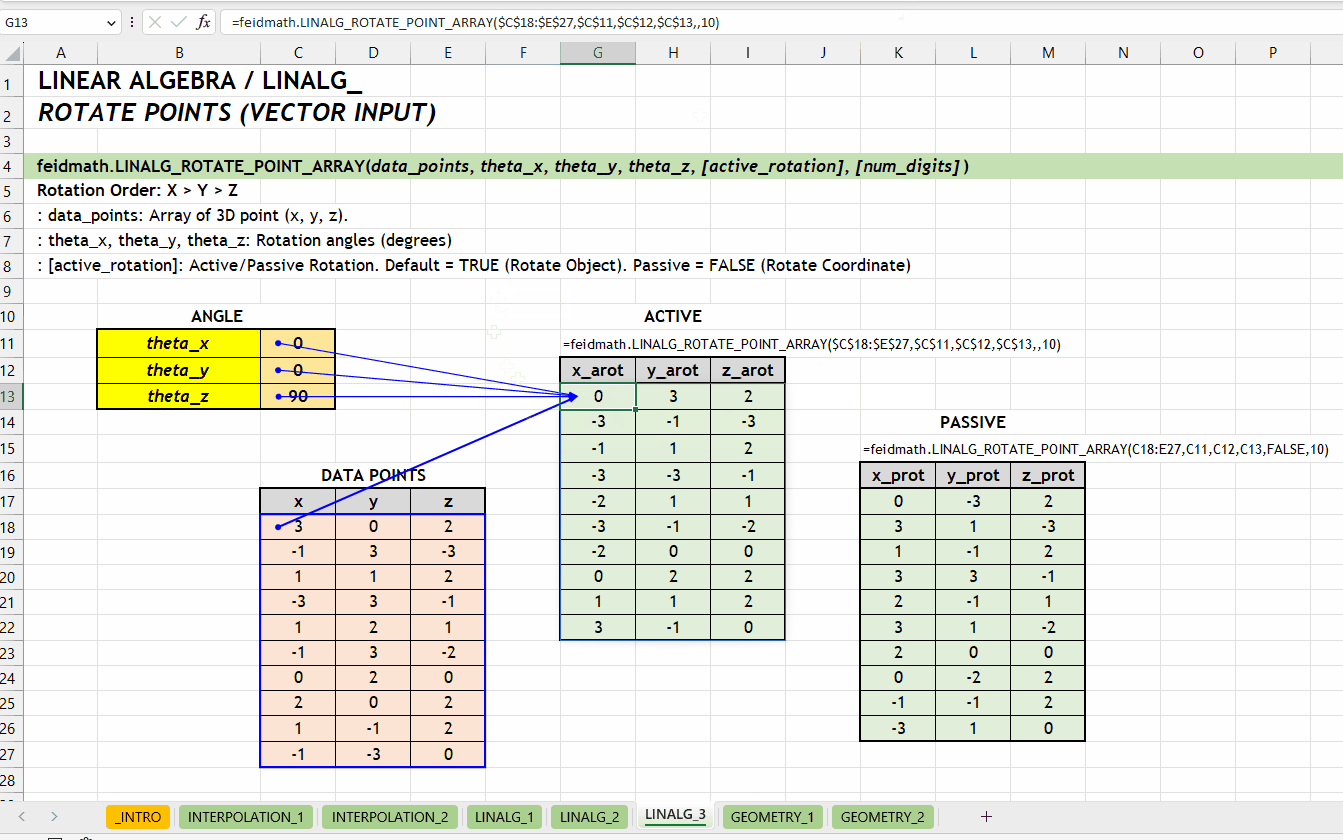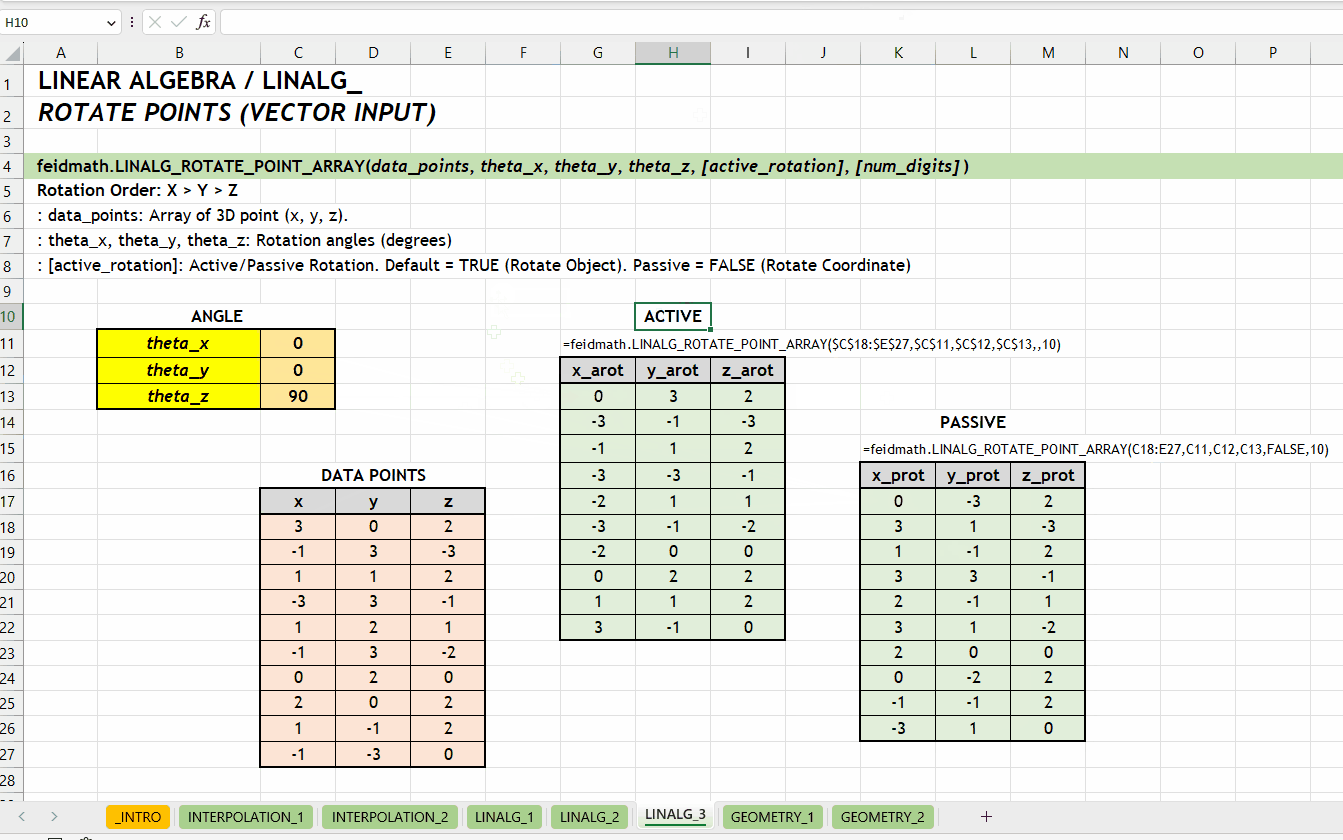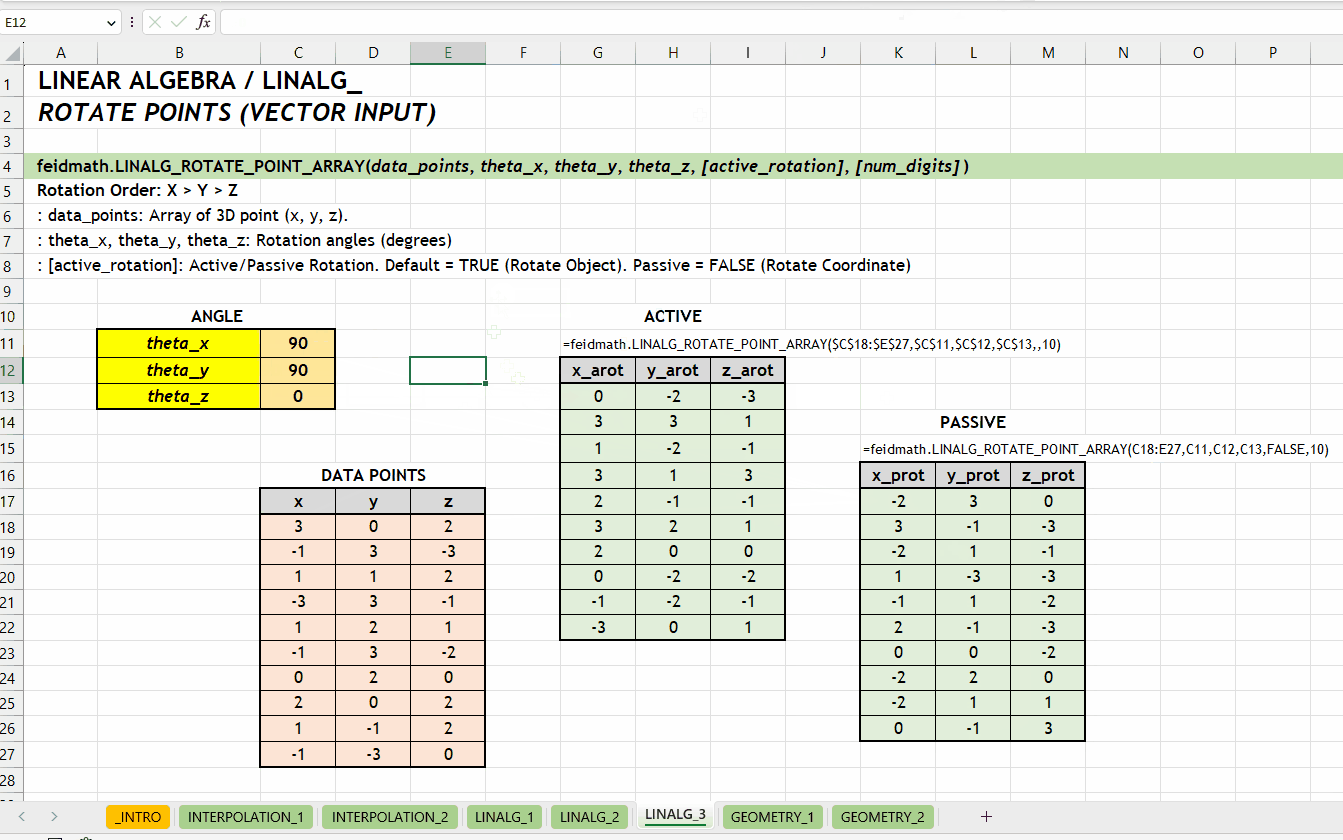
Gambar 3.4: Demonstrasi `LINALG_ROTATE_POINT_ARRAY()`

Visualisasi Aktif vs. Pasif

Berikut visualisasi perbedaan antara merotasikan objek (aktif) dan koordinatnya (pasif). Rotasi terhadap sumbu \(z\) dengan grafik hubungan \(x\) dan \(y\).

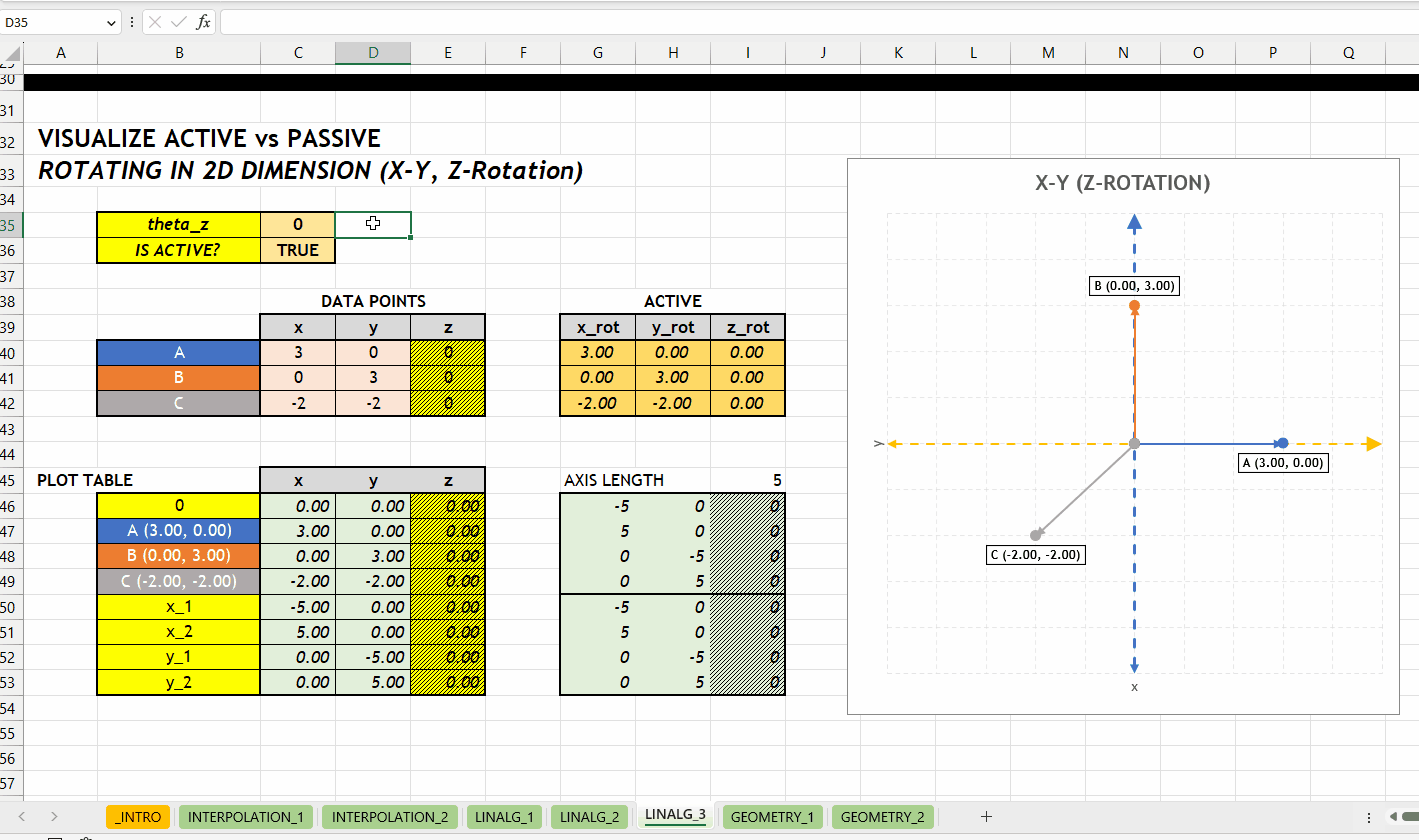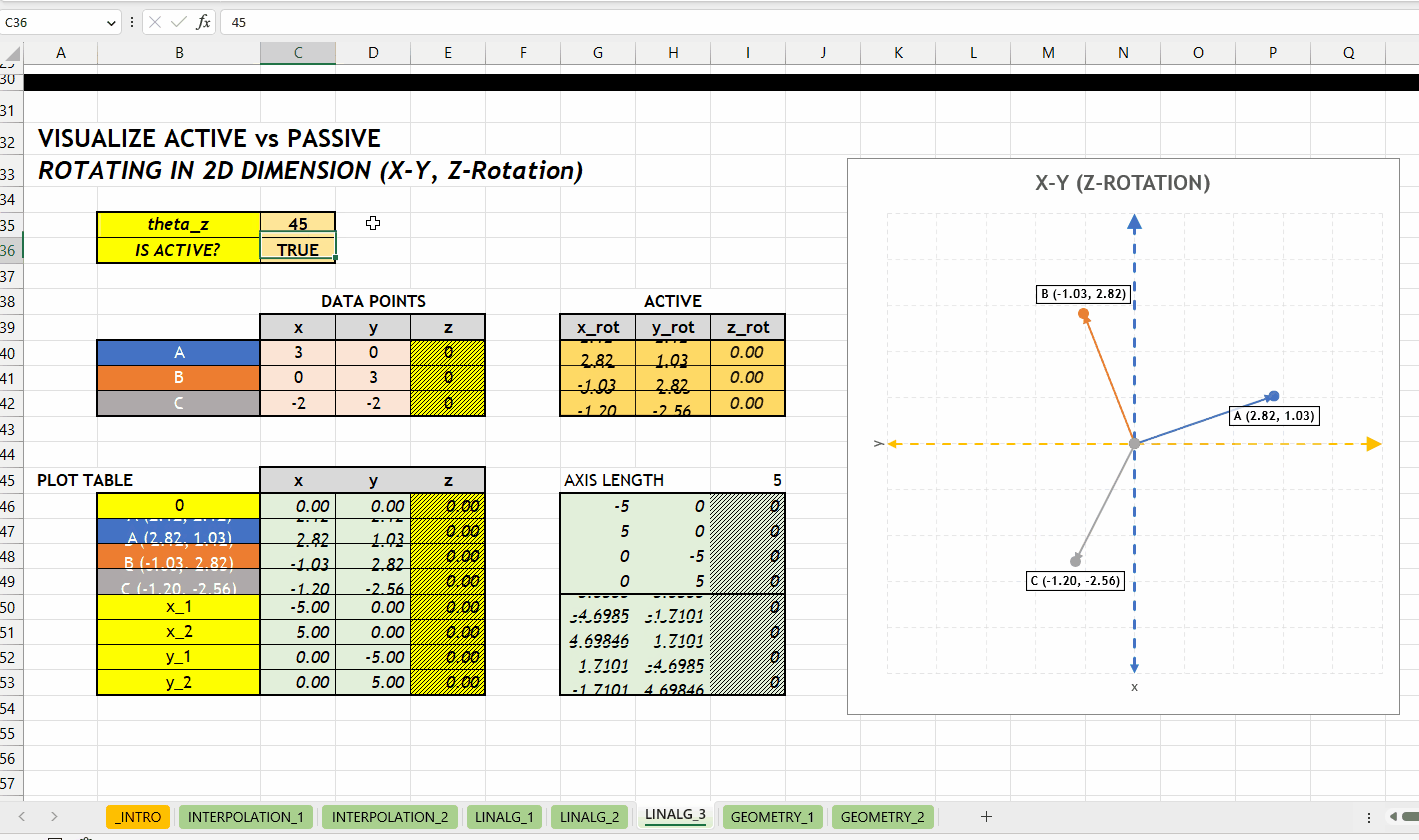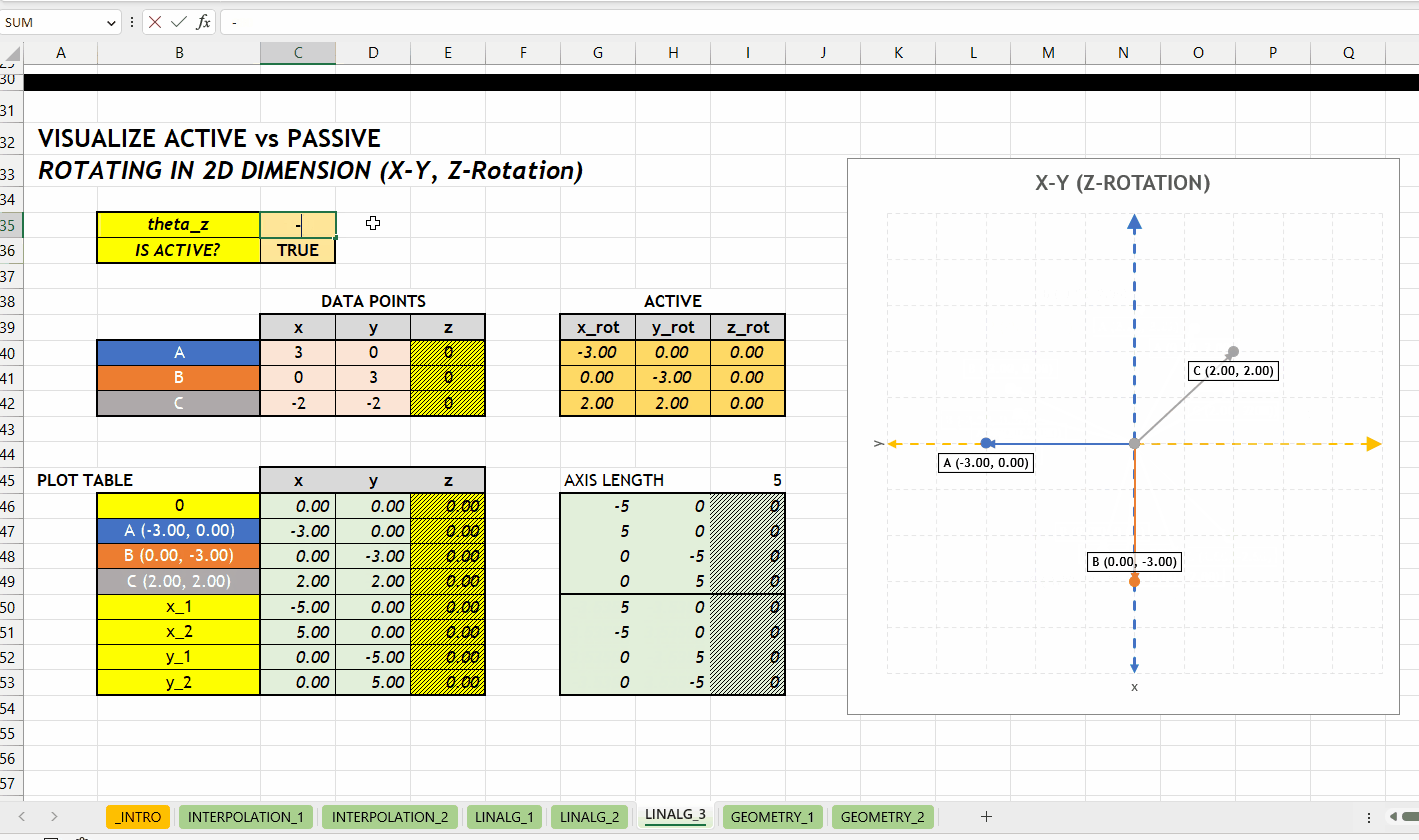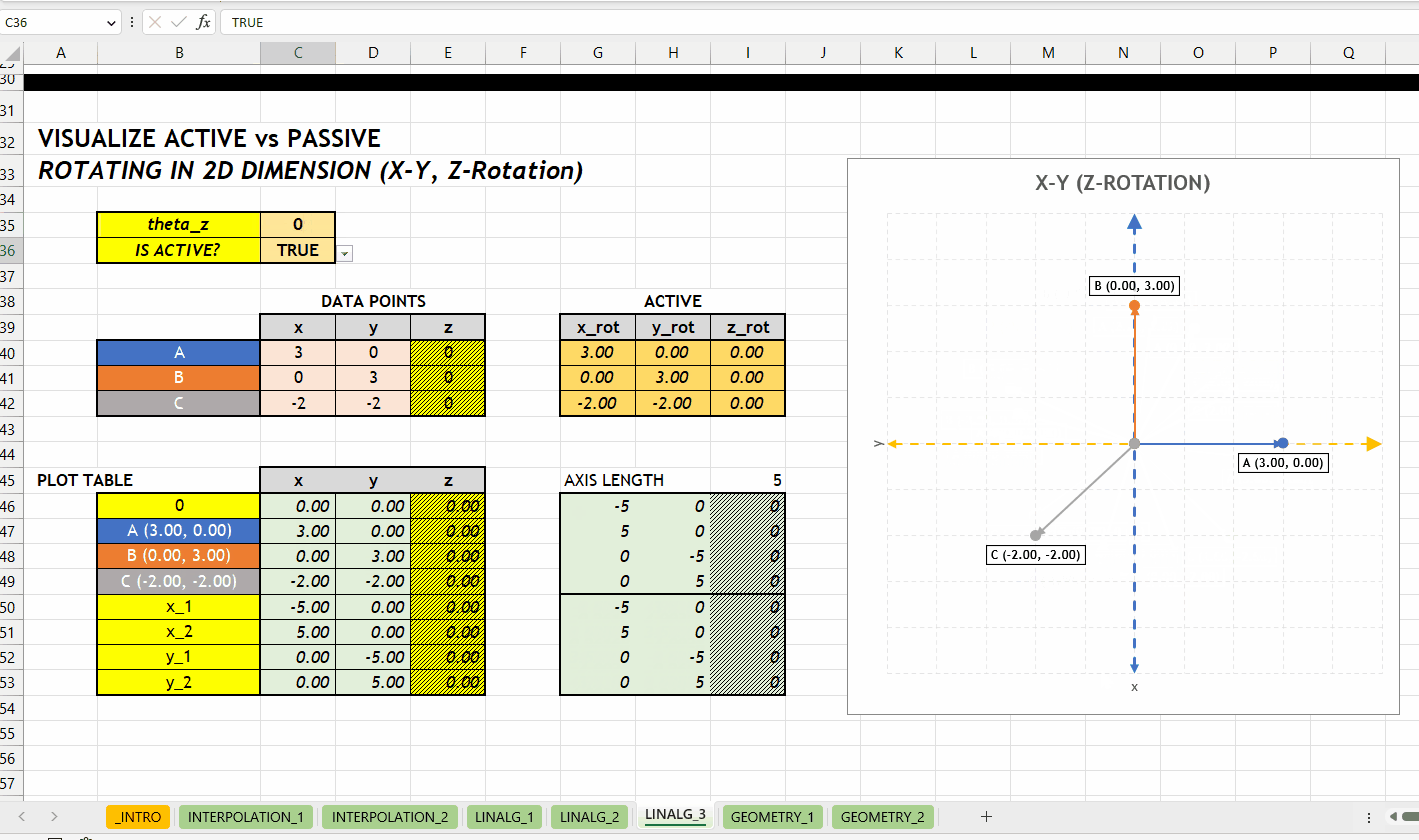
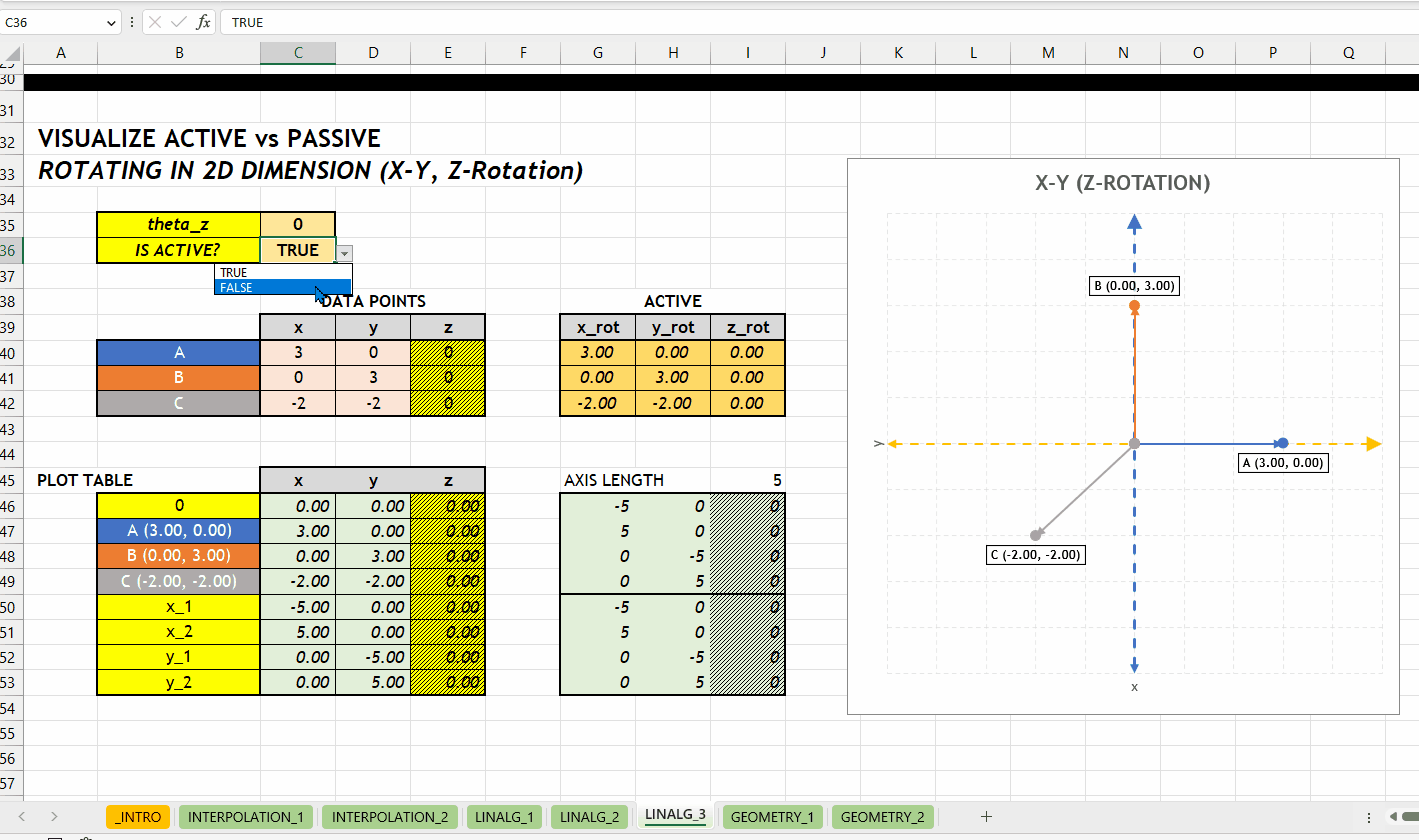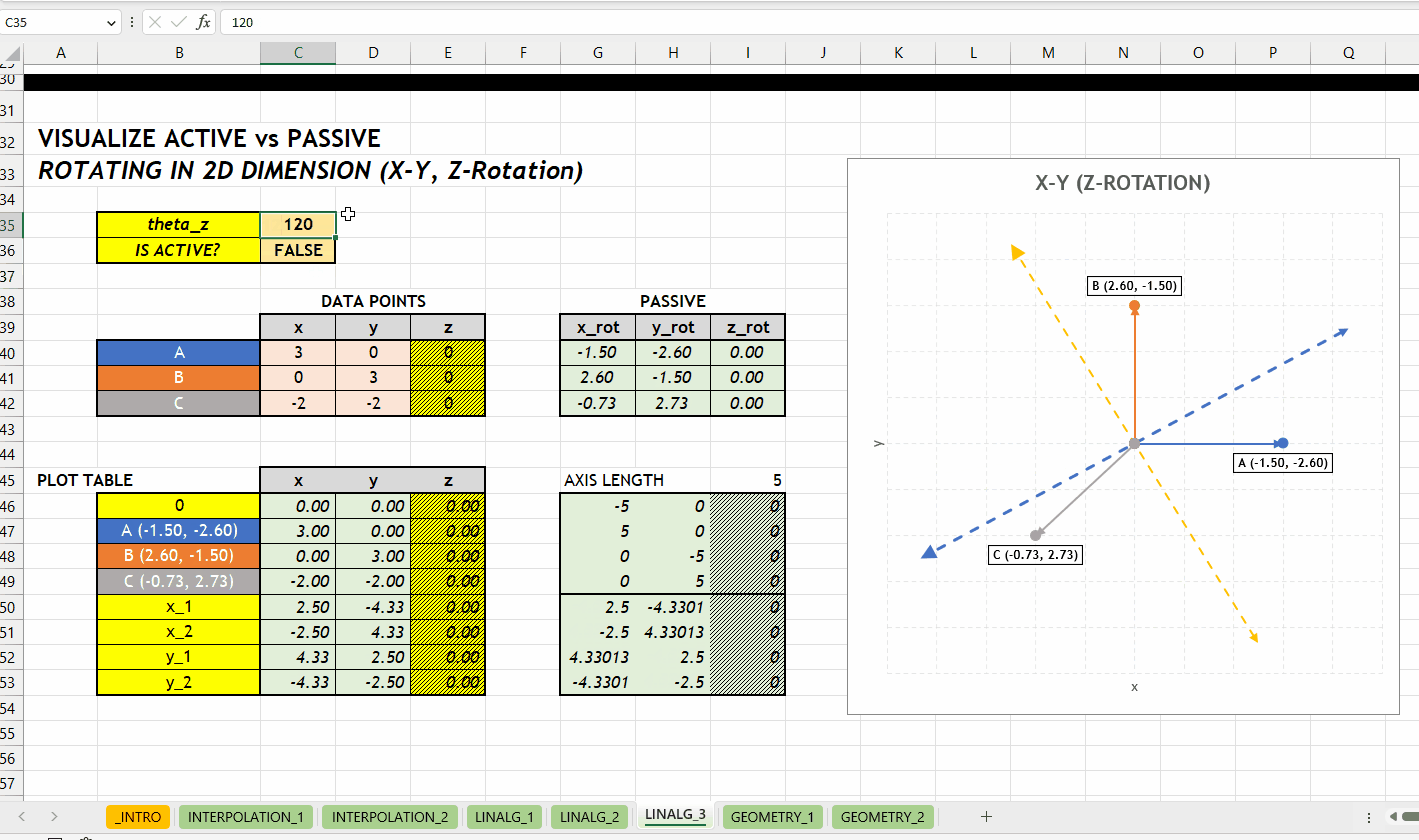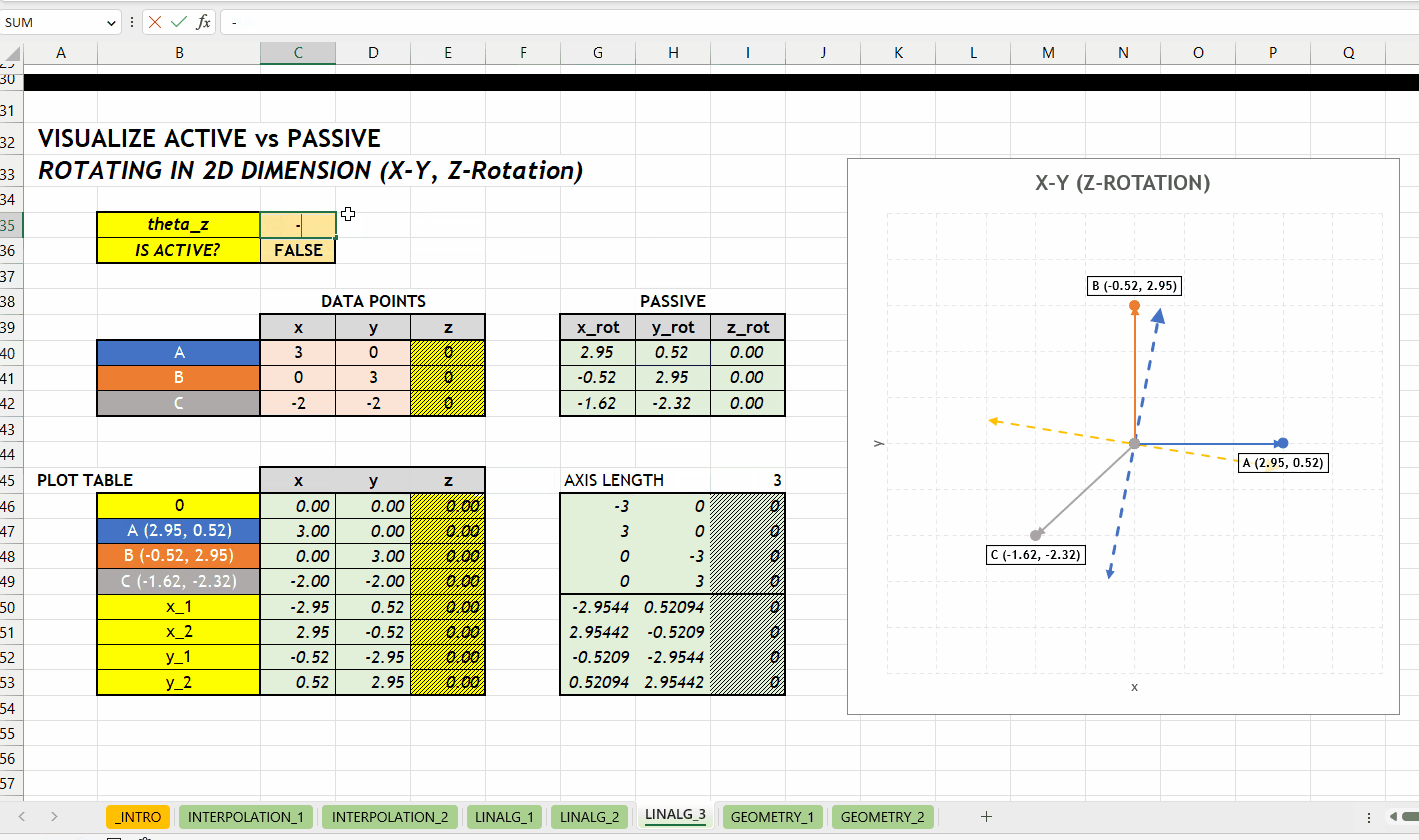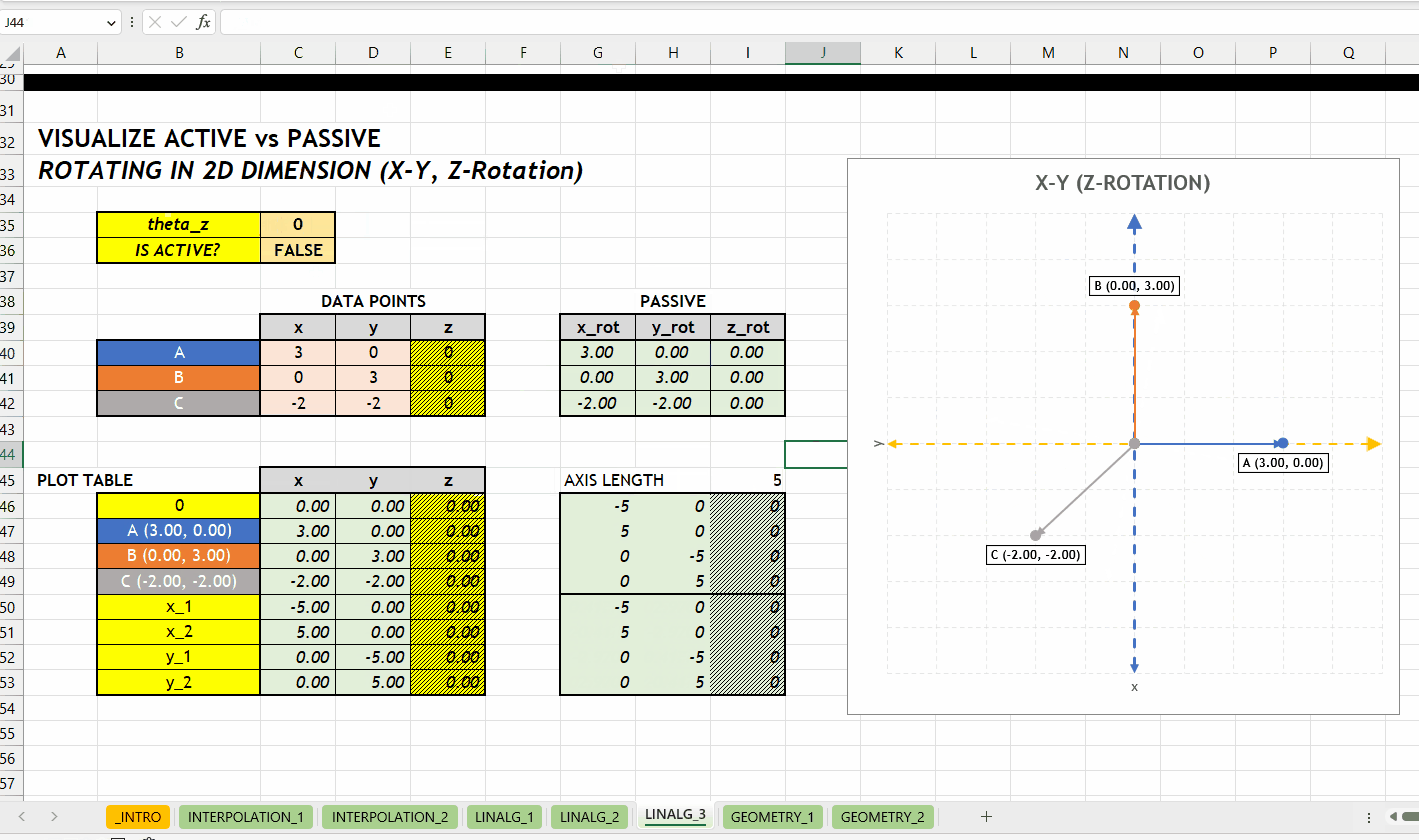
Kategori `GEOMETRY_*`

NEW v0.1 Kategori GEOMETRY_* berisikan fungsi geometri seperti mengidentifikasi titik berada di dalam/luar poligon. Hubungan antar fungsi di kategori ini bisa dilihat di Gambar 4.1.

%%{ init: { 'theme': 'forest' } }%%

flowchart LR
  NONE ---> GEOMETRY_IS_POINT_IN_POLYGON
  GEOMETRY_IS_POINT_IN_POLYGON ---> GEOMETRY_ARE_POINTS_IN_POLYGON

Gambar 4.1: Grafik dependencies kategori GEOMETRY_*

Fungsi utama kategori GEOMETRY_* yaitu GEOMETRY_POINT_IN_POLYGON() dan GEOMETRY_ARE_POINTS_IN_POLYGON().

Source Code GEOMETRY_*

// NONE ---> GEOMETRY_IS_POINT_IN_POLYGON
GEOMETRY_IS_POINT_IN_POLYGON = LAMBDA(point_vector, data_polygon,
    LET(
        point_vector, TOCOL(point_vector),
        xp, INDEX(point_vector, 1),
        yp, INDEX(point_vector, 2),
        data_1, DROP(data_polygon, -1),
        data_2, DROP(data_polygon, 1),
        data_joined, HSTACK(data_1, data_2),
        _x1, CHOOSECOLS(data_joined, 1),
        _y1, CHOOSECOLS(data_joined, 2),
        _x2, CHOOSECOLS(data_joined, 3),
        _y2, CHOOSECOLS(data_joined, 4),
        first_condition, (yp < _y1) <> (yp < _y2),
        second_condition, xp <
            (_x1 + (((yp - _y1) / (_y2 - _y1)) * (_x2 - _x1))),
        final_condition, IFERROR(
            (first_condition * second_condition) = 1,
            FALSE
        ),
        is_inside, MOD(SUM(INT(final_condition)), 2) = 1,
        is_inside
    )
);

// GEOMETRY_IS_POINT_IN_POLYGON ---> GEOMETRY_ARE_POINTS_IN_POLYGON
GEOMETRY_ARE_POINTS_IN_POLYGON = LAMBDA(data_points, polygon_points,
    BYROW(
        data_points,
        LAMBDA(row, GEOMETRY_IS_POINT_IN_POLYGON(row, polygon_points))
    )
);

`GEOMETRY_IS_POINT_IN_POLYGON()`

Fungsi GEOMETRY_IS_POINT_IN_POLYGON(point_vector, polygon_points) digunakan untuk menentukan apakah sebuah titik berada di dalam atau di luar sebuah poligon yang tertutup. Titik yang akan dicek dinyatakan oleh point_vector, sedangkan polygon_points adalah array yang setiap barisnya merepresentasikan titik dari poligon. Fungsi ini mengembalikan nilai boolean/logical, yaitu TRUE jika titik berada di dalam poligon, dan FALSE jika tidak.

Referensi: Fungsi ini dikembangkan berdasarkan video Checking if a point is inside a polygon is RIDICULOUSLY simple (Ray casting algorithm) - Inside code oleh Inside code.

Syntax: GEOMETRY_IS_POINT_IN_POLYGON(point_vector, polygon_points)
Output: logical

point_vector := [number vector]: Koordinat titik yang ingin dicek dalam bentuk vektor (\(x\), \(y\)).
polygon_points := [number array]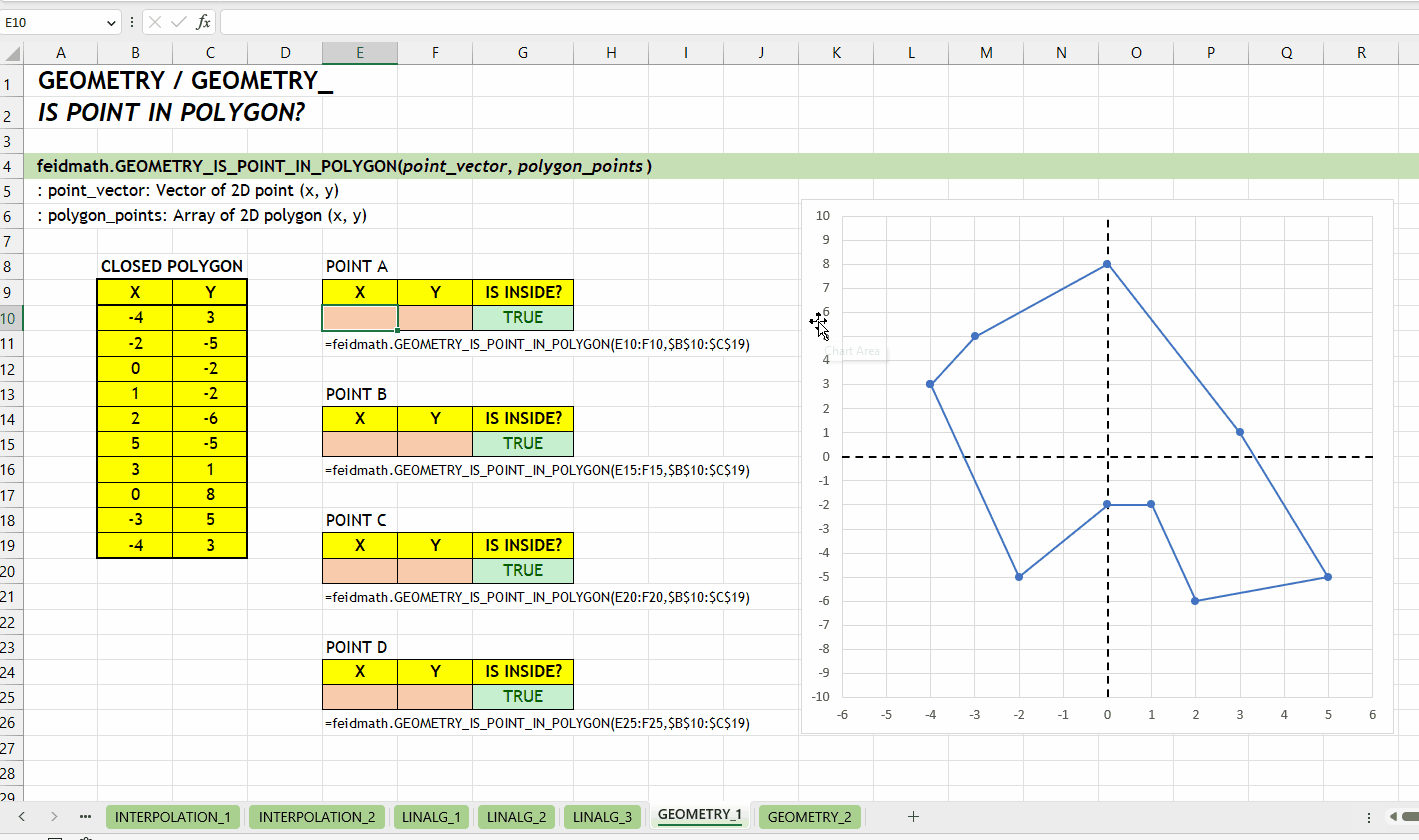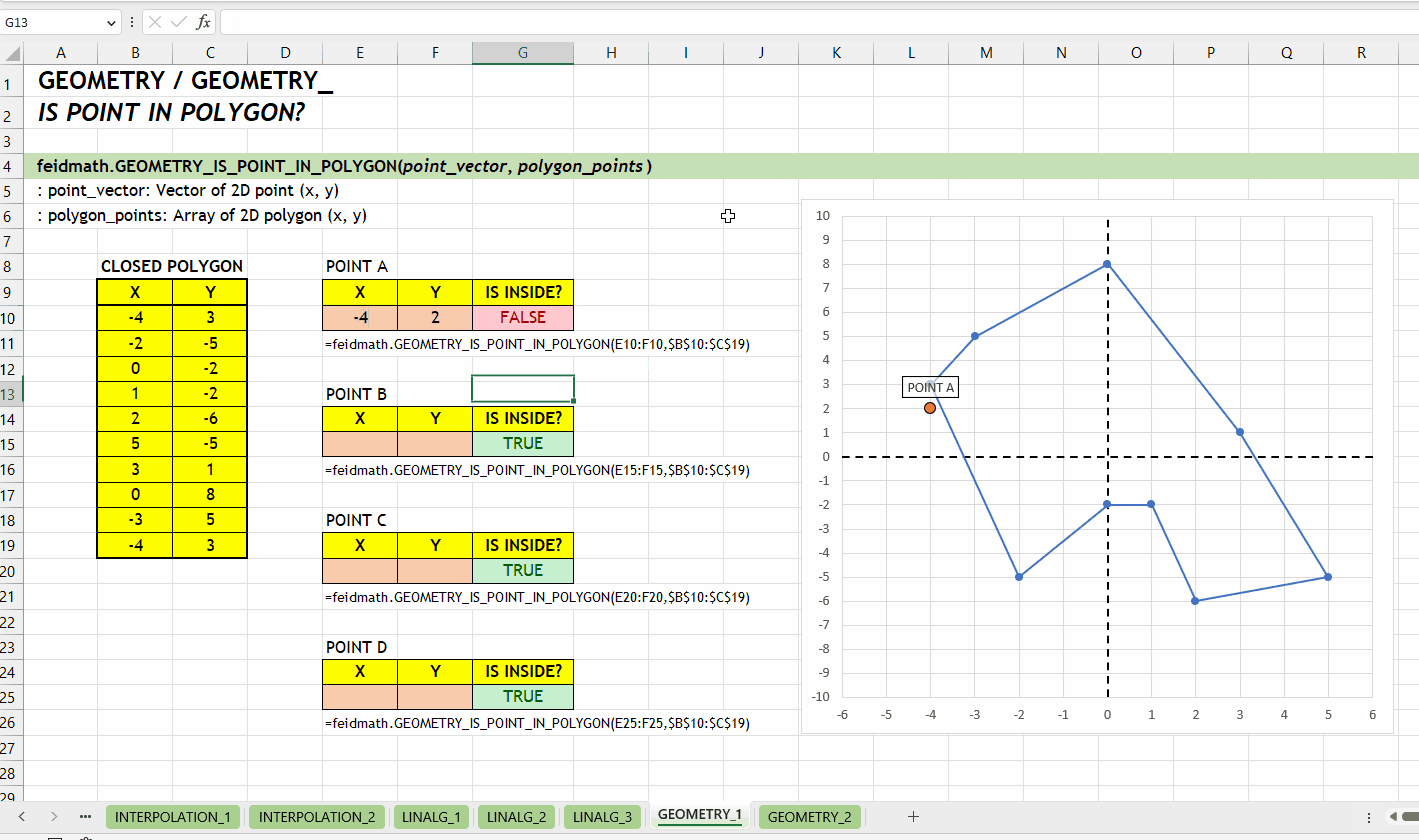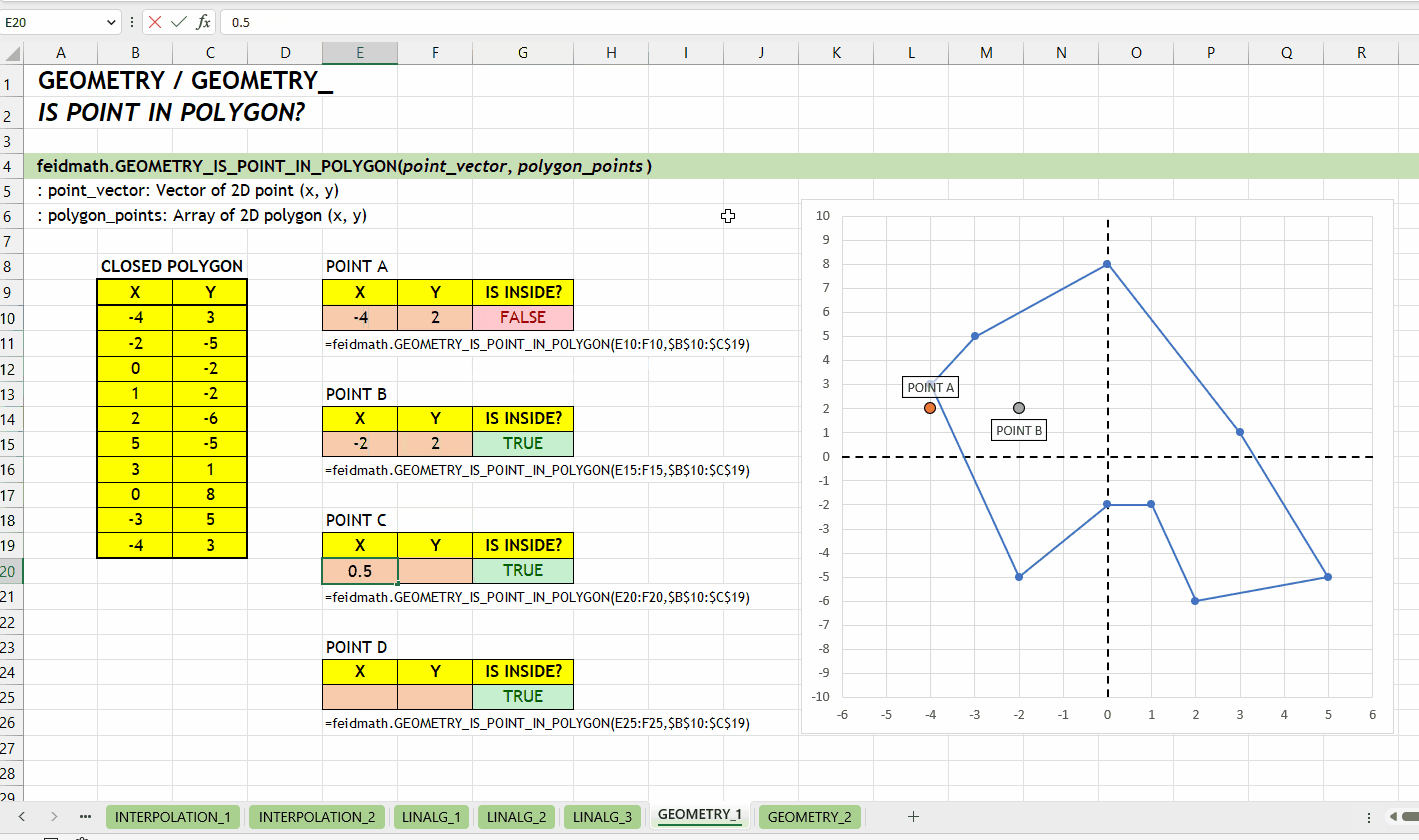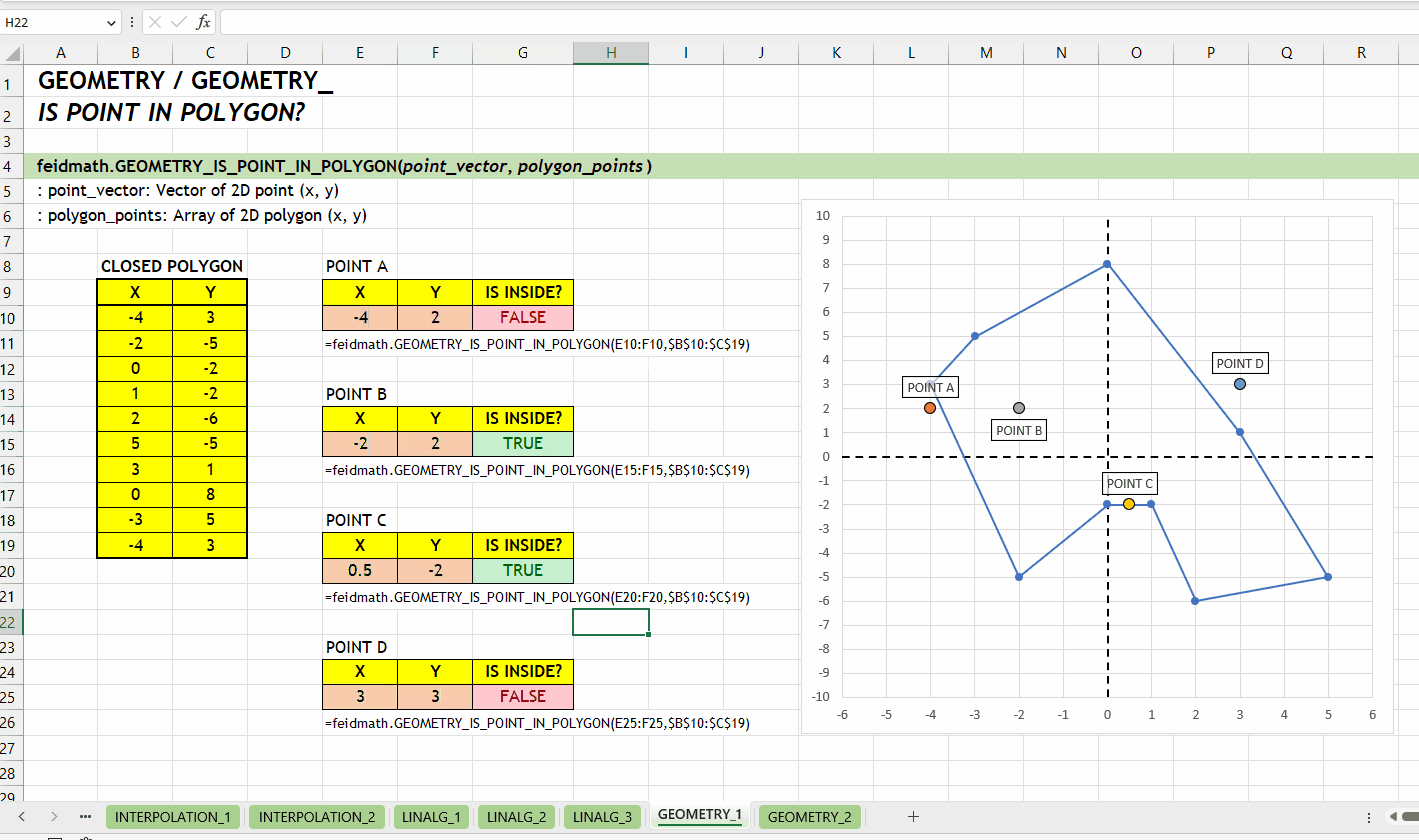: Sekumpulan koordinat titik yang membentuk poligon dalam bentuk array dengan kolom \(x\), \(y\).

Gambar 4.2: Demonstrasi `GEOMETRY_IS_POINT_IN_POLYGON()`

`GEOMETRY_ARE_POINTS_IN_POLYGON()`

Fungsi GEOMETRY_ARE_POINTS_IN_POLYGON(data_points, polygon_points) sama dengan GEOMETRY_IS_POINT_IN_POLYGON() tetapi dirancang untuk mengecek sejumlah titik sekaligus. Argumen data_points harus berupa array yang setiap barisnya merepresentasikan titik yang akan dicek. Seperti halnya fungsi GEOMETRY_IS_POINT_IN_POLYGON(), fungsi ini mengembalikan array nilai boolean, yaitu TRUE untuk titik-titik yang berada di dalam poligon dan FALSE untuk titik-titik yang berada di luar poligon.

Syntax: GEOMETRY_ARE_POINTS_IN_POLYGON(data_points, polygon_points)
Output: logical vector

data_points := [number array]: Sekumpulan koordinat titik yang ingin dicek dalam bentuk array \(m \times 2\) dengan kolom (\(x\), \(y\)).
polygon_points := [number array]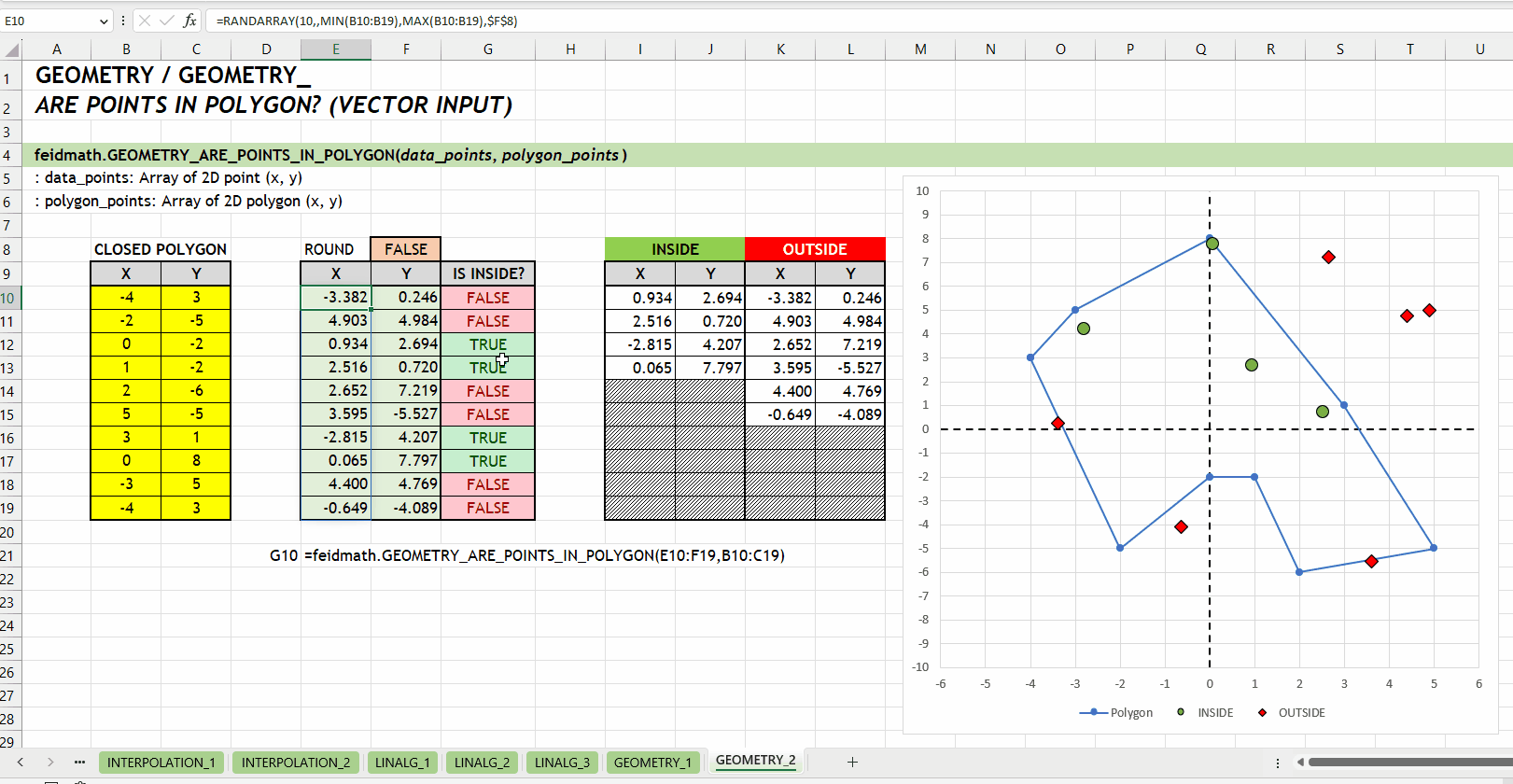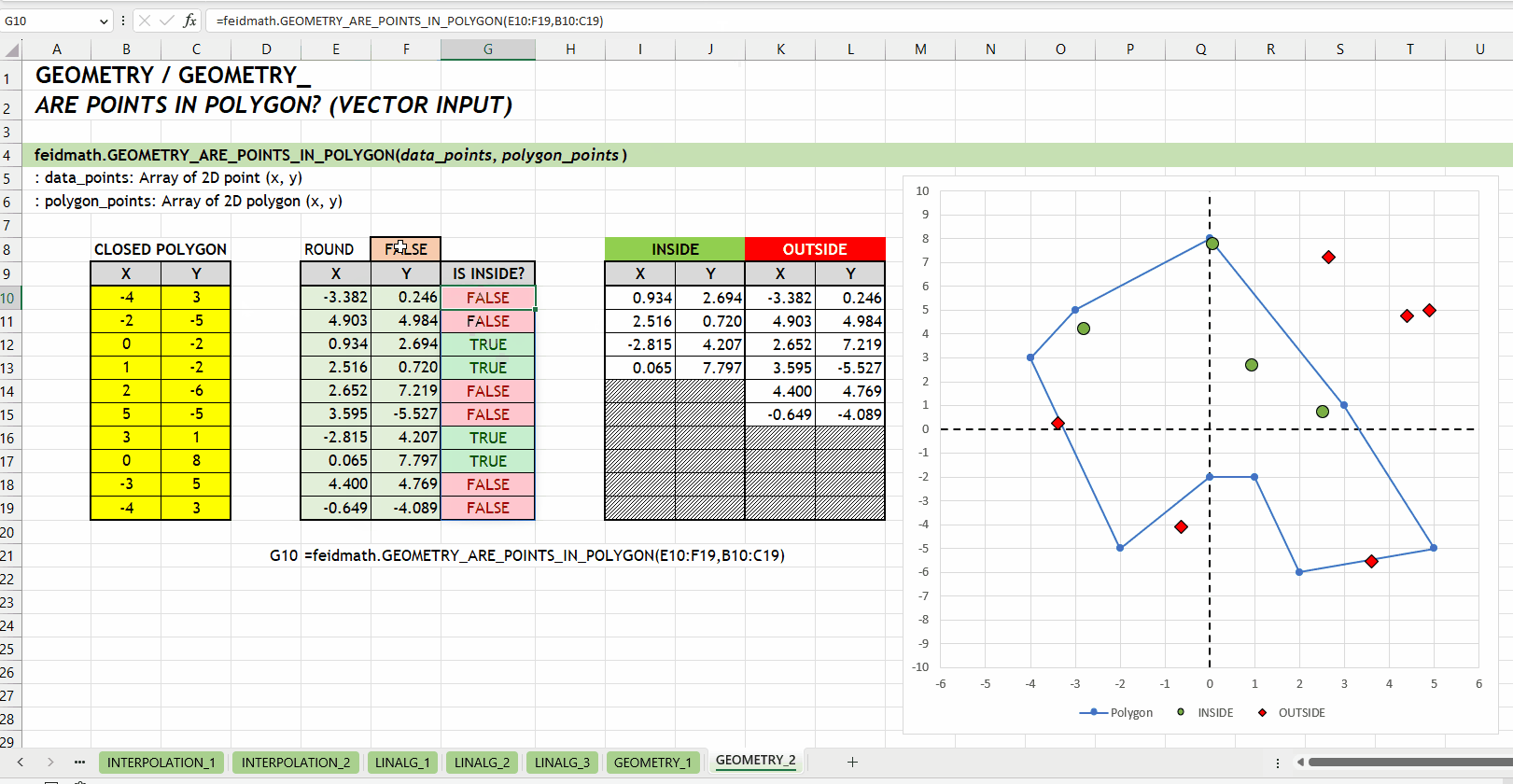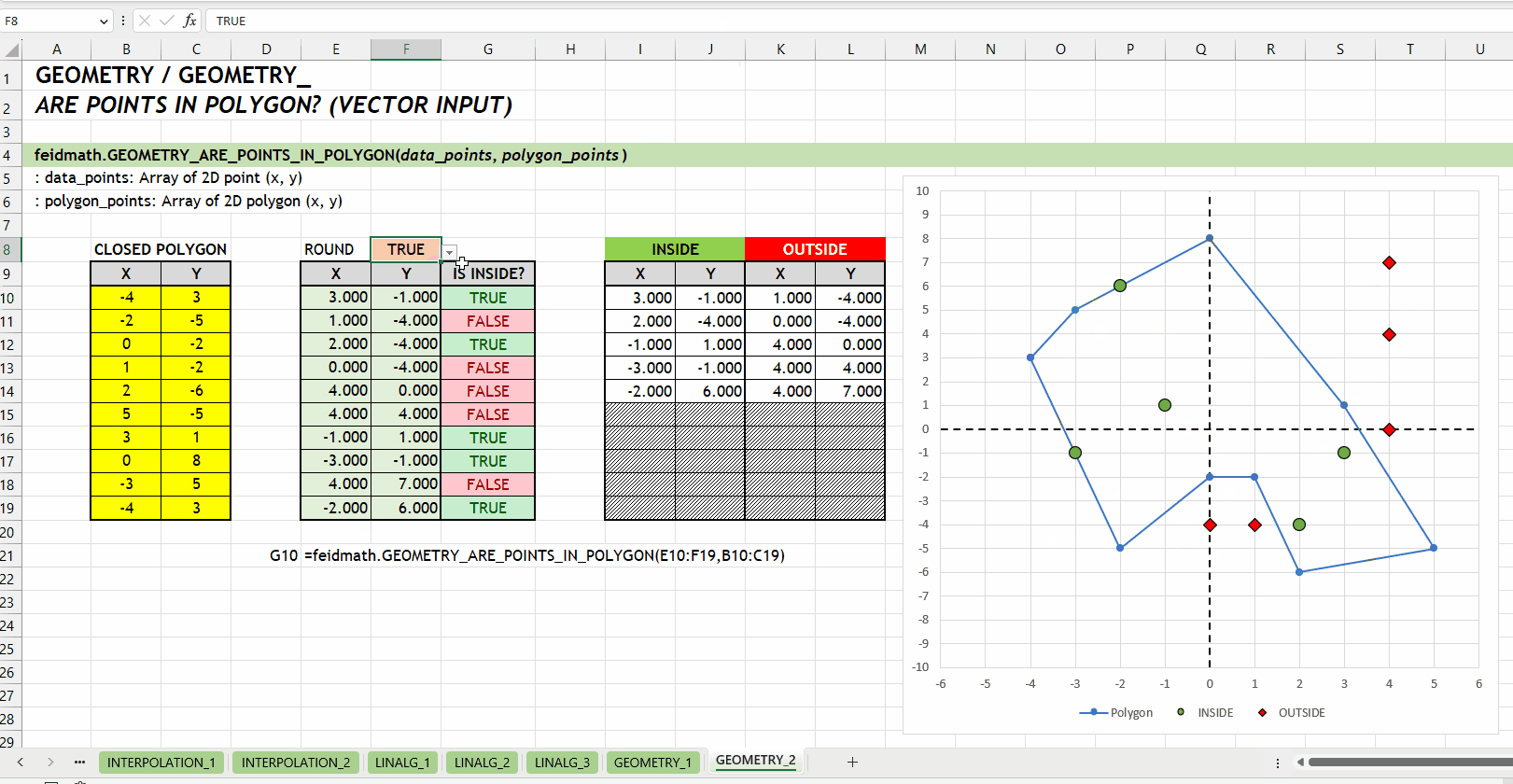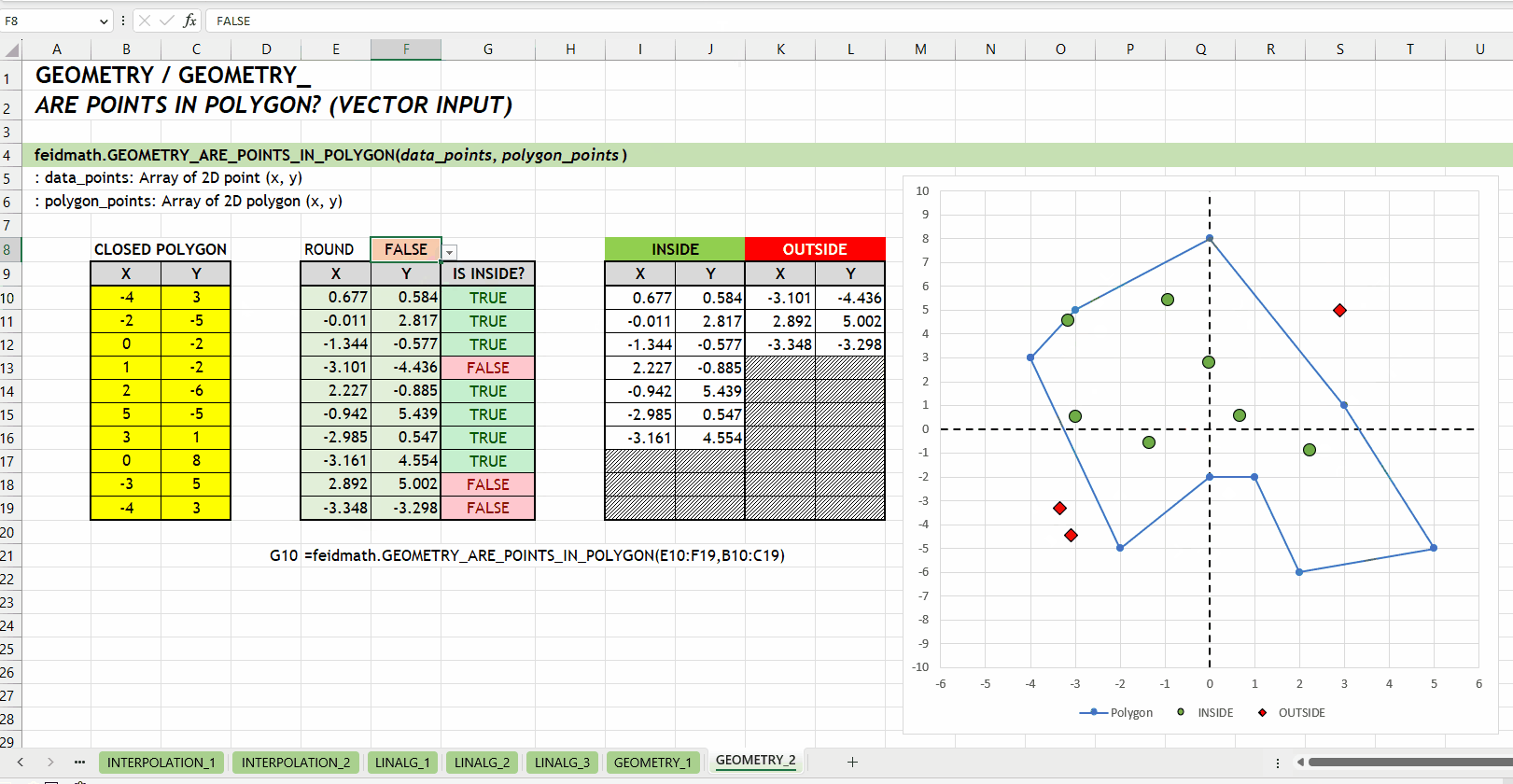: Sekumpulan koordinat titik yang membentuk poligon dalam bentuk array dengan kolom \(x\), \(y\).

Gambar 4.3: Demonstrasi `GEOMETRY_ARE_POINTS_IN_POLYGON()`

Fungsi feidmath v0.1 memiliki \(3\) kategori dengan total \(6\) fungsi utama.

Jika memiliki ide untuk pengembangan feidlambda atau fungsi baru bisa langsung disampaikan dengan membuat isu di github. Dan jika bertemu masalah saat penggunaan feidmath v0.1, bisa juga membuat isu di github.

Changelog

2023-05-26 (v0.1.0)
- Rilis feidmath v0.1
  - Kategori baru: INTERPOLATION
    - Fungsi baru: INTERPOLATION_LINEAR()
  - Kategori baru: LINALG (LINEAR ALGEBRA)
    - Fungsi baru: LINALG_ROTATION_MATRIX()
    - Fungsi baru: LINALG_ROTATE_POINT()
    - Fungsi baru: LINALG_ROTATE_POINT_ARRAY()
  - Kategori baru: GEOMETRY
    - Fungsi baru: GEOMETRY_IS_POINT_IN_POLYGON()
    - Fungsi baru: GEOMETRY_ARE_POINTS_IN_POLYGON()

Fungsi feidmath v0.1.x

Kategori INTERPOLATION_*

INTERPOLATION_LINEAR()

Kategori LINALG_*

LINALG_ROTATION_MATRIX()

LINALG_ROTATE_POINT()

LINALG_ROTATE_POINT_ARRAY()

Visualisasi Aktif vs. Pasif

Kategori GEOMETRY_*

GEOMETRY_IS_POINT_IN_POLYGON()

GEOMETRY_ARE_POINTS_IN_POLYGON()

Changelog

Kategori `INTERPOLATION_*`

`INTERPOLATION_LINEAR()`

Kategori `LINALG_*`

`LINALG_ROTATION_MATRIX()`

`LINALG_ROTATE_POINT()`

`LINALG_ROTATE_POINT_ARRAY()`

Kategori `GEOMETRY_*`

`GEOMETRY_IS_POINT_IN_POLYGON()`

`GEOMETRY_ARE_POINTS_IN_POLYGON()`