Greenhorn:
feidlambda II

Exploring Dynamic Array + User Defined Lambda (UDL)
v1.0 -> 25 Oktober 2022
[v2.0 -> 8 November 2022]

11/8/22

Kegiatan

Greenhorn

Topik

Exploring Dynamic Array and User Defined Lambda (UDL)
Memanfaatkan Dynamic Array dan User-Defined LAMBDA (UDL)

Author

Bahan presentasi dibuat oleh Taruma Sakti Megariansyah

Lisensi

Seluruh materi presentasi menggunakan lisensi CC-BY-NC-SA 4.0

Kontak

hi@taruma.info / team@dev.fiako.engineering

Agenda

Agenda untuk Greenhorn feidlambda II: Exploring Dynamic Array + User Defined Lambda (UDL)

  • Review Daftar Istilah
  • Eksplorasi tentang Logical
  • Dynamic Array Formula (DAF)
  • Fungsi Baru dari Excel 2019 dan 2021
  • User Defined Lambda (UDL)

1 Review Daftar Istilah

Vector dan Array

  • Istilah array dapat diartikan range yang memiliki 1 dimensi atau 2 dimensi.
  • Array dapat dibangkitkan menggunakan sintaks “={...}”. Dengan “,” sebagai pemisah kolom (sepanjang baris), “;” sebagai pemisah baris (sepanjang kolom).

\[ \texttt{{1,2,3}} = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix} , \texttt{{1;2;3}} = \begin{bmatrix} 1\\ 2\\ 3 \end{bmatrix} \]

\[ \texttt{\{} \underbrace{\texttt{1,2,3}}_{\textit{baris ke-}1} \texttt{;} \underbrace{\texttt{4,5,6}}_{\textit{baris ke-}2} \texttt{;} \underbrace{\texttt{7,8,9}}_{\textit{baris ke-}3} \texttt{\}} = \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix} \]

2 Eksplorasi tentang Logical

Eksplorasi mengenai fungsi yang menghasilkan logical yaitu TRUE atau FALSE.

Fungsi Logical

NOT(...), AND(...), OR(...), XOR(...)

Fungsi NOT(...)

NOT (1)

Syntax

=NOT(logical)
  • Fungsi NOT membalikkan nilai argumennya. 1
  • Menghasilkan nilai TRUE ketika kondisi bernilai FALSE, dan berlaku sebaliknya.
  • NOT(TRUE) = FALSE
  • NOT(FALSE) = TRUE

NOT (2)

\[ \texttt{NOT} \left( \begin{bmatrix} \texttt{TRUE}\\ \texttt{FALSE}\\ \texttt{TRUE} \end{bmatrix} \right) = \begin{bmatrix} \texttt{FALSE}\\ \texttt{TRUE}\\ \texttt{FALSE} \end{bmatrix} \]

\[ \texttt{NOT} \left( \begin{bmatrix} \texttt{TRUE} & \texttt{FALSE} & \texttt{TRUE} \end{bmatrix} \right) = \begin{bmatrix} \texttt{FALSE} & \texttt{TRUE} & \texttt{FALSE} \end{bmatrix} \]

\[ \texttt{NOT} \left( \begin{bmatrix} \texttt{TRUE} & \texttt{FALSE}\\ \texttt{FALSE} & \texttt{TRUE}\\ \end{bmatrix} \right) = \begin{bmatrix} \texttt{FALSE} & \texttt{TRUE}\\ \texttt{TRUE} & \texttt{FALSE} \end{bmatrix} \]

Fungsi AND(...)

AND (1)

  • Fungsi logika, untuk menentukan apakah semua kondisi dalam sebuah tes adalah TRUE. 1
=AND(logical1, [logical2], ...)
  • Menghasilkan nilai TRUE ketika seluruh kondisi bernilai TRUE. Jika terdapat satu atau lebih bernilai FALSE maka menghasilkan nilai FALSE.
  • Jika input berupa logical array saja (AND(logical_array)), maka akan mengevaluasi seluruh elemen pada logical array (AND(elemen_1, elemen_2, ...)).

AND (2)

\[ \texttt{AND} \left( \texttt{TRUE}, \texttt{TRUE} \right) = \texttt{AND} \left( \texttt{TRUE}, \texttt{TRUE}, \texttt{TRUE} \right) = \texttt{TRUE} \]

\[ \texttt{AND} \left( \texttt{TRUE}, \texttt{FALSE} \right) = \texttt{AND} \left( \texttt{TRUE}, \texttt{FALSE}, \texttt{TRUE} \right) = \texttt{FALSE} \]

\[ \texttt{AND} \left( \texttt{FALSE}, \texttt{FALSE} \right) = \texttt{AND} \left( \texttt{FALSE}, \texttt{FALSE}, \texttt{FALSE} \right) = \texttt{FALSE} \]

AND (3)

\[ \texttt{AND} \left( \begin{bmatrix} \texttt{TRUE} & \texttt{FALSE} & \texttt{TRUE} \end{bmatrix} \right) = \texttt{AND} \left( \texttt{TRUE}, \texttt{FALSE}, \texttt{TRUE} \right) = \texttt{FALSE} \]

\[ \texttt{AND} \left( \begin{bmatrix} \texttt{TRUE} \\ \texttt{TRUE} \\ \texttt{TRUE} \end{bmatrix} \right) = \texttt{AND} \left( \texttt{TRUE}, \texttt{TRUE}, \texttt{TRUE} \right) = \texttt{TRUE} \]

\[ \texttt{AND} \left( \begin{bmatrix} \texttt{TRUE} & \texttt{FALSE} \\ \texttt{FALSE} & \texttt{TRUE} \end{bmatrix} \right) = \texttt{AND} \left( \texttt{TRUE}, \texttt{FALSE}, \texttt{FALSE}, \texttt{TRUE} \right) = \texttt{FALSE} \]

\[ \texttt{AND} \left( \begin{bmatrix} \texttt{TRUE} \\ \texttt{FALSE} \end{bmatrix} , \begin{bmatrix} \texttt{TRUE} \\ \texttt{FALSE} \end{bmatrix} \right) = \texttt{AND} \left( \texttt{TRUE}, \texttt{FALSE}, \texttt{TRUE}, \texttt{FALSE} \right) = \texttt{FALSE} \]

Fungsi OR(...)

OR (1)

  • Fungsi logika, untuk menentukan apakah salah satu kondisi dalam sebuah tes adalah TRUE. 1
=OR(logical1, [logical2], ...)
  • Menghasilkan nilai TRUE ketika salah satu kondisi bernilai TRUE.
  • Jika input berupa logical array saja (OR(logical_array)), maka akan mengevaluasi seluruh elemen pada logical array (OR(elemen_1, elemen_2, ...)).

OR (2)

\[ \texttt{OR} \left( \texttt{TRUE}, \texttt{TRUE} \right) = \texttt{OR} \left( \texttt{TRUE}, \texttt{TRUE}, \texttt{TRUE} \right) = \texttt{TRUE} \]

\[ \texttt{OR} \left( \texttt{TRUE}, \texttt{FALSE} \right) = \texttt{OR} \left( \texttt{TRUE}, \texttt{FALSE}, \texttt{TRUE} \right) = \texttt{TRUE} \]

\[ \texttt{OR} \left( \texttt{FALSE}, \texttt{FALSE} \right) = \texttt{OR} \left( \texttt{FALSE}, \texttt{FALSE}, \texttt{FALSE} \right) = \texttt{FALSE} \]

OR (3)

\[ \texttt{OR} \left( \begin{bmatrix} \texttt{TRUE} & \texttt{FALSE} & \texttt{TRUE} \end{bmatrix} \right) = \texttt{OR} \left( \texttt{TRUE}, \texttt{FALSE}, \texttt{TRUE} \right) = \texttt{TRUE} \]

\[ \texttt{OR} \left( \begin{bmatrix} \texttt{TRUE} \\ \texttt{TRUE} \\ \texttt{TRUE} \end{bmatrix} \right) = \texttt{OR} \left( \texttt{TRUE}, \texttt{TRUE}, \texttt{TRUE} \right) = \texttt{TRUE} \]

\[ \texttt{OR} \left( \begin{bmatrix} \texttt{TRUE} & \texttt{FALSE} \\ \texttt{FALSE} & \texttt{TRUE} \end{bmatrix} \right) = \texttt{OR} \left( \texttt{TRUE}, \texttt{FALSE}, \texttt{FALSE}, \texttt{TRUE} \right) = \texttt{TRUE} \]

\[ \texttt{OR} \left( \begin{bmatrix} \texttt{TRUE} \\ \texttt{FALSE} \end{bmatrix} , \begin{bmatrix} \texttt{TRUE} \\ \texttt{FALSE} \end{bmatrix} \right) = \texttt{OR} \left( \texttt{TRUE}, \texttt{FALSE}, \texttt{TRUE}, \texttt{FALSE} \right) = \texttt{TRUE} \]

Fungsi XOR(...)

XOR (1)

  • Fungsi XOR mengembalikan logika Exclusive Or dari semua argumen. 1
=XOR(logical1, [logical2], ...)
  • Menghasilkan nilai TRUE ketika hanya satu kondisi bernilai TRUE.
  • Jika input berupa logical array saja (XOR(logical_array)), maka akan mengevaluasi seluruh elemen pada logical array (XOR(elemen_1, elemen_2, ...)).

XOR (2)

\[ \texttt{XOR} \left( \texttt{TRUE}, \texttt{TRUE} \right) = \texttt{XOR} \left( \texttt{TRUE}, \texttt{TRUE}, \texttt{TRUE} \right) = \texttt{FALSE} \]

\[ \texttt{XOR} \left( \texttt{TRUE}, \texttt{FALSE} \right) = \texttt{XOR} \left( \texttt{TRUE}, \texttt{FALSE}, \texttt{FALSE} \right) = \texttt{TRUE} \]

\[ \texttt{XOR} \left( \texttt{TRUE}, \texttt{FALSE}, \texttt{TRUE} \right) = \texttt{FALSE} \]

\[ \texttt{XOR} \left( \texttt{FALSE}, \texttt{FALSE} \right) = \texttt{XOR} \left( \texttt{FALSE}, \texttt{FALSE}, \texttt{FALSE} \right) = \texttt{FALSE} \]

XOR (3)

\[ \texttt{XOR} \left( \begin{bmatrix} \texttt{TRUE} & \texttt{FALSE} & \texttt{TRUE} \end{bmatrix} \right) = \texttt{XOR} \left( \texttt{TRUE}, \texttt{FALSE}, \texttt{TRUE} \right) = \texttt{FALSE} \]

\[ \texttt{XOR} \left( \begin{bmatrix} \texttt{TRUE} \\ \texttt{FALSE} \\ \texttt{FALSE} \end{bmatrix} \right) = \texttt{XOR} \left( \texttt{TRUE}, \texttt{FALSE}, \texttt{FALSE} \right) = \texttt{TRUE} \]

\[ \texttt{XOR} \left( \begin{bmatrix} \texttt{TRUE} & \texttt{FALSE} \\ \texttt{FALSE} & \texttt{TRUE} \end{bmatrix} \right) = \texttt{XOR} \left( \texttt{TRUE}, \texttt{FALSE}, \texttt{FALSE}, \texttt{TRUE} \right) = \texttt{FALSE} \]

\[ \texttt{XOR} \left( \begin{bmatrix} \texttt{TRUE} \\ \texttt{FALSE} \end{bmatrix} , \begin{bmatrix} \texttt{FALSE} \\ \texttt{FALSE} \end{bmatrix} \right) = \texttt{XOR} \left( \texttt{TRUE}, \texttt{FALSE}, \texttt{FALSE}, \texttt{FALSE} \right) = \texttt{TRUE} \]

Logical \(\iff\) Number

Logical \(\Rightarrow\) Number (1)

  • \(\texttt{FALSE} = 0\). Bernilai FALSE jika bernilai 0. \(\{ x = 0 \}\)

  • \(\texttt{TRUE} \neq 0\). Bernilai TRUE jika nilai bukan 0. \(\{ x \in \mathbb{R}\ |\ x \neq 0 \}\)

  • Mengubah logical menjadi number dapat menggunakan fungsi INT(...). 1

  • \(\texttt{INT}(\texttt{TRUE}) = 1\).

  • \(\texttt{INT}(\texttt{FALSE}) = 0\).

Logical dan operator aritmatika (1)

  • Logical array akan diubah menjadi numeric array ketika bertemu operator aritmatika (+, *, -, /).
  • Perubahan logical menjadi number sama dengan proses penggunaan fungsi INT(...).
  • Operator aritmatika perkalian (* / \(\times\)) dan penambahan (+) dapat berperilaku seperti fungsi logical AND (*) dan OR (+).
  • Umumnya operator perkalian setiap elemen dalam suatu vector atau matriks (array) menggunakan simbol \(\odot\). Akan tetapi, pada materi ini simbol \(\times\) diartikan sebagai perkalian setiap elemen (element-wise) dan bukan perkalian matriks.

Logical dan operator aritmatika (2)

\[ \mathbf{X} \underbrace{\textsf{ operator }}_{\times\ |\ +} \mathbf{Y} \Rightarrow \mathbf{P} \underbrace{\textsf{ operator }}_{\times\ |\ +} \mathbf{Q} \]

\[ \mathbf{X} \in \mathbb{B}_l, \mathbf{Y} \in \mathbb{B}_l, \mathbf{P} \in \mathbb{B}_i, \mathbf{Q} \in \mathbb{B}_i \]

  • Simbol \(\mathbb{B}\) untuk menyatakan nilai logical atau boolean. 1

\[ \mathbb{B}_l = \{ \texttt{TRUE, FALSE} \} = \{ \text{T}, \text{F} \} , \mathbb{B}_i = \{ 0, 1 \} \]

\[ \overbrace{ \begin{bmatrix} \texttt{TRUE}\\ \texttt{FALSE}\\ \texttt{FALSE} \end{bmatrix} }^{\text{logical array}} \underbrace{\ \times\ |\ +\ }_\text{operator} \overbrace{ \begin{bmatrix} \texttt{TRUE}\\ \texttt{TRUE}\\ \texttt{FALSE} \end{bmatrix} }^{\text{logical array}} \Rightarrow \overbrace{ \begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix} }^{\text{numeric array}} \underbrace{\ \times\ |\ +\ }_\text{operator} \overbrace{ \begin{bmatrix} 1\\ 1\\ 0 \end{bmatrix} }^{\text{numeric array}} \]

Operator perkalian

Operator perkalian * sebagai AND (1)

  • Setiap nilai yang dikalikan dengan 0 akan bernilai 0.

\[ x \times 0 = 0,\ \{x \in \mathbb{R}\} \]

  • Setiap nilai yang dikalikan dengan FALSE akan bernilai FALSE.

Operator perkalian * sebagai AND (2)

\[ \begin{bmatrix} \texttt{TRUE}\\ \texttt{FALSE}\\ \texttt{FALSE} \end{bmatrix} \times \begin{bmatrix} \texttt{TRUE}\\ \texttt{TRUE}\\ \texttt{FALSE} \end{bmatrix} \Rightarrow \begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix} \times \begin{bmatrix} 1\\ 1\\ 0 \end{bmatrix} = \underbrace{ \begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix} }_{\textit{hasil akhir}} \]

\[ \Rightarrow \underbrace{ \left( \begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix} \neq 0 \right) }_{\textit{mengubah menjadi logical}} = \begin{bmatrix} \texttt{TRUE}\\ \texttt{FALSE}\\ \texttt{FALSE} \end{bmatrix} \]

Operator penambahan

Operator penambahan + sebagai OR (1)

  • Berlaku seperti penambahan pada umumnya.

\[ x + 0 = x, x \in \mathbb{R} \]

\[ x + y = x + y, x \in \mathbb{R}, y \in \mathbb{R} \]

  • Setiap nilai yang bukan 0 bernilai TRUE. \(\texttt{TRUE} \neq 0\)

Operator penambahan + sebagai OR (2)

\[ \begin{bmatrix} \texttt{TRUE}\\ \texttt{FALSE}\\ \texttt{FALSE} \end{bmatrix} + \begin{bmatrix} \texttt{TRUE}\\ \texttt{TRUE}\\ \texttt{FALSE} \end{bmatrix} \Rightarrow \begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix} + \begin{bmatrix} 1\\ 1\\ 0 \end{bmatrix} = \underbrace{ \begin{bmatrix} 2\\ 1\\ 0 \end{bmatrix} }_{\textit{hasil akhir}} \]

\[ \Rightarrow \underbrace{ \left( \begin{bmatrix} 2\\ 1\\ 0 \end{bmatrix} \neq 0 \right) }_{\textit{mengubah menjadi logical}} = \begin{bmatrix} \texttt{TRUE}\\ \texttt{TRUE}\\ \texttt{FALSE} \end{bmatrix} \]

Number \(\Rightarrow\) Logical

Number \(\Rightarrow\) Logical (1)

  • Numeric array dapat digunakan sebagai kondisi logical.
  • Setiap numeric array yang digunakan sebagai conditional secara tidak langsung berubah menjadi logical array.
  • Perubahan tersebut sama saja jika membandingkan array tidak sama dengan 0. \[ \left( \mathbf{x}_{\text{number}} \neq 0 \right) = \mathbf{x}_{\text{logical}} \]

Number \(\Rightarrow\) Logical (2)

\[ \texttt{NOT} \left( \underbrace{ \begin{bmatrix} 3\\ -1\\ 0 \end{bmatrix} }_{\textit{numeric}} \equiv 0 \right) = \left( \underbrace{ \begin{bmatrix} 3\\ -1\\ 0 \end{bmatrix} }_{\textit{numeric}} \neq 0 \right) = \underbrace{ \begin{bmatrix} \texttt{TRUE}\\ \texttt{TRUE}\\ \texttt{FALSE} \end{bmatrix} }_{\textit{logical}} \]

  • Sama saja dengan formula =NOT(array=0) atau =array<>0.

Number \(\Rightarrow\) Logical (2)

\[ \texttt{IF} \left( \underbrace{ \begin{bmatrix} 3\\ -1\\ 0 \end{bmatrix} }_{\textit{numeric}} , \underbrace{\dots}_{\texttt{TRUE}} , \underbrace{\dots}_{\texttt{FALSE}} \right) \Rightarrow \texttt{IF} \left( \underbrace{ \begin{bmatrix} \texttt{TRUE}\\ \texttt{TRUE}\\ \texttt{FALSE} \end{bmatrix} }_{\textit{logical}} , \underbrace{\dots}_{\texttt{TRUE}} , \underbrace{\dots}_{\texttt{FALSE}} \right) \]

Yang perlu diperhatikan

  • Hasil dari logical array bertemu dengan operator aritmatika selalu numeric array.

\[ \begin{bmatrix} \texttt{TRUE}\\ \texttt{FALSE}\\ \texttt{FALSE} \end{bmatrix} \times \begin{bmatrix} \texttt{TRUE}\\ \texttt{TRUE}\\ \texttt{FALSE} \end{bmatrix} + \begin{bmatrix} \texttt{FALSE}\\ \texttt{TRUE}\\ \texttt{TRUE} \end{bmatrix} \Rightarrow \begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix} \times \begin{bmatrix} 1\\ 1\\ 0 \end{bmatrix} + \begin{bmatrix} 0\\ 1\\ 1 \end{bmatrix} = \begin{bmatrix} 1\\ 1\\ 1 \end{bmatrix} \]

  • Jika numeric array digunakan sebagai argumen conditional, maka akan dikonversikan menjadi logical array.

Mengenal Fungsi IS*(...)

Kumpulan fungsi logika untuk mevalidasi input.

Fungsi IS*(...)

SYNTAX

=IS*(value)
  • Memeriksa nilai tertentu dan mengembalikan TRUE atau FALSE bergantung pada hasilnya. 1
  • ISBLANK(...) bernilai TRUE jika sel kosong.
  • ISNUMBER(...) bernilai TRUE jika sel berisikan angka.

Koleksi Fungsi IS*

Periksa error / kosong

  • ISNA(...): Cek nilai apakah #N/A.
  • ISERR(...): Cek nilai apakah error selain #N/A (#VALUE!, #REF!, #DIV/0!, #NUM!, #NAME?, atau #NULL!).
  • ISERROR(...): Cek nilai apakah error (seluruh jenis error).
  • ISBLANK(...): Cek nilai apakah kosong.

Periksa jenis sel

  • ISLOGICAL(...): Cek nilai apakah logical (TRUE atau FALSE).
  • ISNUMBER(...): Cek nilai apakah angka (\(\mathbb{R}\)).
  • ISTEXT(...): Cek nilai apakah teks. Dan ISNONTEXT(...): Cek niai apakah bukan teks (number, logical, error)
  • ISFORMULA(...): Cek nilai apakah formula.

Periksa jenis bilangan

  • ISEVEN(...): Cek nilai apakah bilangan genap.
  • ISODD(...): Cek nilai apakah bilangan ganjil.

Validasi input dengan ISNUMBER(...)

Validasi dengan ISNUMBER(...) (1)

\[ f : \mathbb{R} \to \mathbb{R} \]

\[ f(\mathbf{x}) = \mathbf{y} = \mathbf{x} + 2 \]

\[ \mathbf{x} \in \mathbb{R}, \mathbf{y} \in \mathbb{R} \]

\[ \mathbf{x} \mapsto \mathbf{x} + 2 \]

  • Umumnya nilai \(\mathbf{y}\) dihitung dengan formula =x+2 dengan asumsi \(\mathbf{x}\) bernilai angka \(\{ \mathbf{x} \in \mathbb{R} \}\).

\[ \mathbf{x} = \begin{bmatrix} 3 \\ 2 \\ 7 \end{bmatrix} \mapsto f(\mathbf{x}) = \begin{bmatrix} 3 \\ 2 \\ 7 \end{bmatrix} + 2 = \begin{bmatrix} 5 \\ 4 \\ 9 \end{bmatrix} \]

Validasi dengan ISNUMBER(...) (2)

  • Bagaimana jika \(\mathbf{x}\) memiliki elemen yang bukan angka yaitu text / error / logical?

\[ \mathbf{x} = \begin{bmatrix} 3 \\ \textrm{bob} \\ 2 \end{bmatrix} \mapsto f(\mathbf{x}) = \begin{bmatrix} 3 \\ \textrm{bob} \\ 2 \end{bmatrix} + 2 = \begin{bmatrix} 5 \\ \texttt{#VALUE!} \\ 2 \end{bmatrix} \]

Validasi dengan ISNUMBER(...) (3)

  • Validasi input menggunakan ISNUMBER(...)

\[ \mathbf{x} = \begin{bmatrix} 3 \\ \textrm{bob} \\ 2 \end{bmatrix} \mapsto \texttt{ISNUMBER} \left( \mathbf{x} \right) = \texttt{ISNUMBER} \left( \begin{bmatrix} 3 \\ \textrm{bob} \\ 2 \end{bmatrix} \right) = \begin{bmatrix} \texttt{TRUE} \\ \texttt{FALSE} \\ \texttt{TRUE} \end{bmatrix} \]

\[ \begin{bmatrix} \texttt{TRUE} \\ \texttt{FALSE} \\ \texttt{TRUE} \end{bmatrix} \mapsto \texttt{AND} \left( \mathbf{x} \right) = \texttt{AND} \left( \begin{bmatrix} \texttt{TRUE} \\ \texttt{FALSE} \\ \texttt{TRUE} \end{bmatrix} \right) = \texttt{FALSE} \]

\[ \mathbf{x} \mapsto \texttt{AND}( \texttt{ISNUMBER}( \mathbf{x} ) ) = \texttt{AND}( \texttt{ISNUMBER}( \begin{bmatrix} 3 \\ \textrm{bob} \\ 2 \end{bmatrix} ) ) = \texttt{FALSE} \]

Validasi dengan ISNUMBER(...) (4)

\[ \begin{equation} \mathbf{x} \mapsto \texttt{AND} ( \texttt{ISNUMBER}(\mathbf{x}) ) = \begin{cases} \texttt{TRUE} & f : \mathbf{x} \in \mathbb{R} \rightarrow \mathbb{R}\\ \texttt{FALSE} & \textrm{return}\ \texttt{#VALUE!} \\ \texttt{FALSE} & \mathbf{x} \mapsto g(\mathbf{x}) = \texttt{FILTER}(\dots) \mapsto \\ & f: g(\mathbf{x}) \in \mathbb{R} \rightarrow \mathbb{R}\\ \end{cases} \end{equation} \]

  • Validasi ini dapat diimplementasikan ketika terdapat ketidakpastian jika \(\mathbf{x}\) dapat bernilai bukan angka (\(\mathbf{x} \in \mathbb{R} \lor \mathbf{x} \notin \mathbb{R}\))
  • Solusi lain dengan melakukan filter pada \(\mathbf{x}\) dan hanya mengambil elemen yang angka dengan FILTER(...).

3 Dynamic Array Formula (DAF)

Koleksi fungsi baru (Excel 2021) yang memanfaatkan dynamic array.

Menyeleksi/memilih data

Menggunakan FILTER(...) dan UNIQUE(...)

FILTER(...) (1)

  • FILTER(...): Fungsi FILTER memungkinkan Anda memfilter rentang data berdasarkan kriteria yang ditetapkan. 1
=FILTER(array, include, [if_empty])
  • Argumen include harus berupa vector (kolom atau baris). dan jumlah kolom/baris harus sama dengan array.
  • Argumen if_empty dapat diisi dengan nilai ketika argumen include kosong atau FALSE.

FILTER(...) (2)

\[ \texttt{FILTER} \left( \underbrace{ \begin{bmatrix} 10 & 8\\ \textit{A} & -100\\ -3 & \textit{y} \end{bmatrix} }_{\texttt{array}} , \underbrace{ \overbrace{ \begin{bmatrix} \texttt{TRUE}\\ \texttt{FALSE}\\ \texttt{TRUE} \end{bmatrix} }^{\textit{logical column vector}} }_{\texttt{include}} \right) = \underbrace{ \begin{bmatrix} 10 & 8\\ -3 & \textit{y} \end{bmatrix} }_{\textit{hasil}} \]

\[ \texttt{FILTER} \left( \underbrace{ \begin{bmatrix} 10 & 8\\ \textit{A} & -100\\ -3 & \textit{y} \end{bmatrix} }_{\texttt{array}} , \underbrace{ \overbrace{ \begin{bmatrix} \texttt{FALSE} & \texttt{TRUE} \end{bmatrix} }^{\textit{logical row vector}} }_{\texttt{include}} \right) = \underbrace{ \begin{bmatrix} 8\\ -100\\ \textit{y} \end{bmatrix} }_{\textit{hasil}} \]

FILTER(...) (3)

\[ \texttt{FILTER} \left( \underbrace{ \begin{bmatrix} 10 & 8\\ \textit{A} & -100\\ -3 & \textit{y} \end{bmatrix} }_{\texttt{array}} , \underbrace{ \overbrace{ \begin{bmatrix} \texttt{FALSE}\\ \texttt{FALSE}\\ \texttt{FALSE} \end{bmatrix} }^{\textit{logical column vector}} }_{\texttt{include}} , \underbrace{ \textrm{tidak ada} }_{\texttt{if_empty}} \right) = \textrm{tidak ada} \]

FILTER(...) (4)

\[ \texttt{array} = \mathbf{A} \rightarrow \mathbf{A} \in \mathbb{U}^{m \times n}, \{m, n \in \mathbb{N}\ |\ m, n \neq 0 \} \]

\[ \mathbb{U} = \{ \textrm{seluruh nilai } u \textrm{ yang dapat digunakan di Excel}\} \]

  • \(m\) menunjukkan jumlah baris dan \(n\) menunjukkan jumlah kolom.

\[ \texttt{include} = \mathbf{i} \rightarrow \mathbf{i} \in \mathbb{B}^{k}, \{k = m \lor k = n\} \]

  • \(\mathbf{i}\) selalu berupa logical vector dengan jumlah baris/kolom \(k\) sama dengan \(m \lor n\).

UNIQUE(...) (1)

  • UNIQUE(...): Fungsi UNIQUE menghasilkan daftar nilai yang unik dalam daftar atau rentang. 1
=UNIQUE(array, [by_col], [exactly_once])
  • Penggunaan argumen by_col untuk mencari nilai unik untuk setiap baris atau kolom. Nilai default argumen by_col <- FALSE.
  • Argumen exactly_once dapat digunakan untuk menyaring nilai unik yang muncul lebih dari satu kali. Jika exactly_once <- TRUE, maka jika terdapat nilai unik yang muncul dua kali akan dihapus. Nilai default argumen exactly_once <- FALSE.

UNIQUE(...) (2)

\[ \texttt{UNIQUE} \left( \underbrace{ \overbrace{ \begin{bmatrix} 1 & 1 & 3 & 1\\ 4 & 2 & 7 & 2\\ 3 & 2 & 8 & 2\\ 1 & 1 & 3 & 1\\ 5 & 2 & 9 & 2 \end{bmatrix} }^{\textit{array / vector}} }_{\texttt{array}} \right) \Rightarrow \underbrace{ \begin{bmatrix} 1 & 1 & 3 & 1\\ 4 & 2 & 7 & 2\\ 3 & 2 & 8 & 2\\ 5 & 2 & 9 & 2 \end{bmatrix} }_{\textit{hasil}} \]

UNIQUE(...) (3)

\[ \texttt{UNIQUE} \left( \underbrace{ \overbrace{ \begin{bmatrix} 1 & 1 & 3 & 1\\ 4 & 2 & 7 & 2\\ 3 & 2 & 8 & 2\\ 1 & 1 & 3 & 1\\ 5 & 2 & 9 & 2 \end{bmatrix} }^{\textit{array / vector}} }_{\texttt{array}} , \underbrace{ \texttt{ TRUE } }_{\texttt{by_col}} \right) \Rightarrow \underbrace{ \begin{bmatrix} 1 & 1 & 3\\ 4 & 2 & 7\\ 3 & 2 & 8\\ 1 & 1 & 3\\ 5 & 2 & 9 \end{bmatrix} }_{\textit{hasil}} \]

UNIQUE(...) (4)

\[ \texttt{UNIQUE} \left( \underbrace{ \overbrace{ \begin{bmatrix} 1 & 1 & 3 & 1\\ 4 & 2 & 7 & 2\\ 3 & 2 & 8 & 2\\ 1 & 1 & 3 & 1\\ 5 & 2 & 9 & 2 \end{bmatrix} }^{\textit{array / vector}} }_{\texttt{array}} , \underbrace{ \texttt{ FALSE } }_{\texttt{by_col}} , \underbrace{ \texttt{ TRUE } }_{\texttt{exactly_once}} \right) \Rightarrow \underbrace{ \begin{bmatrix} 4 & 2 & 7 & 2\\ 3 & 2 & 8 & 2\\ 5 & 2 & 9 & 2 \end{bmatrix} }_{\textit{hasil}} \]

Membangkitkan data

Menggunakan SEQUENCE(...) dan RANDARRAY(...).

SEQUENCE(...) (1)

  • SEQUENCE(...): Fungsi SEQUENCE memungkinkan Anda menghasilkan daftar angka yang berurutan dalam larik seperti \({1, 2, 3, 4, \dots}\). 1
=SEQUENCE(rows, [columns], [start], [step])
  • Hasil SEQUENCE(...) => numeric vector/array.
  • Nilai default argumen: columns <- 1, start <- 1, step <- 1.

SEQUENCE(...) (2)

\[ \texttt{SEQUENCE} \left( \underbrace{ 5 }_{\texttt{rows}} \right) \Rightarrow \underbrace{ \begin{bmatrix} 1\\ 2\\ 3\\ 4\\ 5 \end{bmatrix} }_{\textit{hasil}} \]

\[ \texttt{SEQUENCE} \left( \underbrace{ 3 }_{\texttt{rows}} , \underbrace{ 4 }_{\texttt{columns}} \right) \Rightarrow \underbrace{ \begin{bmatrix} 1 & 2 & 3 & 4\\ 5 & 6 & 7 & 8\\ 9 & 10 & 11 & 12 \end{bmatrix} }_{\textit{hasil}} \]

SEQUENCE(...) (3)

\[ \texttt{SEQUENCE} \left( \underbrace{ 3 }_{\texttt{rows}} , \underbrace{ 4 }_{\texttt{columns}} , \underbrace{ 10 }_{\texttt{start}} \right) \Rightarrow \underbrace{ \begin{bmatrix} 10 & 11 & 12 & 13\\ 14 & 15 & 16 & 17\\ 18 & 19 & 20 & 21\\ \end{bmatrix} }_{\textit{hasil}} \]

\[ \texttt{SEQUENCE} \left( \underbrace{ 3 }_{\texttt{rows}} , \underbrace{ 4 }_{\texttt{columns}} , \underbrace{ 10 }_{\texttt{start}} , \underbrace{ 3 }_{\texttt{step}} \right) \Rightarrow \underbrace{ \begin{bmatrix} 10 & 13 & 16 & 19\\ 22 & 25 & 28 & 31\\ 34 & 37 & 40 & 43\\ \end{bmatrix} }_{\textit{hasil}} \]

RANDARRAY(...) (1)

  • RANDARRAY(...): Fungsi RANDARRAY menghasilkan larik angka acak. Anda dapat menentukan jumlah baris dan kolom yang akan diisi, nilai minimum dan maksimum, dan apakah fungsi mengembalikan bilangan bulat atau nilai desimal. 1
=RANDARRAY([rows], [columns], [min], [max], [whole_number])
  • Nilai default argumen: rows <- 1, columns <- 1, min <- 0, max <- 1, whole_number <- FALSE.
  • Jika tidak diisi argumen maka hasil RANDARRAY() adalah bilangan real \(\mathbb{R}\) acak dengan rentang \([0, 1]\).

RANDARRAY(...) (2)

\[ \texttt{RANDARRAY} \left( \underbrace{ 3 }_{\texttt{rows}} \right) \Rightarrow \underbrace{ \begin{bmatrix} 0.036290129\\ 0.831941087\\ 0.596526220 \end{bmatrix} }_{\textit{hasil}} \]

\[ \texttt{RANDARRAY} \left( \underbrace{ 3 }_{\texttt{rows}} , \underbrace{ 2 }_{\texttt{columns}} \right) \Rightarrow \underbrace{ \begin{bmatrix} 0.950708256 & 0.044725252\\ 0.111202134 & 0.34866703\\ 0.119602266 & 0.792763221 \end{bmatrix} }_{\textit{hasil}} \]

RANDARRAY(...) (3)

\[ \texttt{RANDARRAY} \left( \underbrace{ 3 }_{\texttt{rows}} , \underbrace{ 2 }_{\texttt{columns}} , \underbrace{ 3 }_{\texttt{min}} , \underbrace{ 10 }_{\texttt{max}} \right) \Rightarrow \underbrace{ \begin{bmatrix} 5.033450196 & 7.903953859\\ 7.918426053 & 6.750036234\\ 7.926034250 & 3.596169723\\ \end{bmatrix} }_{\textit{hasil}} \]

\[ \texttt{RANDARRAY} \left( \underbrace{ 3 }_{\texttt{rows}} , \underbrace{ 2 }_{\texttt{columns}} , \underbrace{ 3 }_{\texttt{min}} , \underbrace{ 10 }_{\texttt{max}} , \underbrace{ \texttt{ TRUE } }_{\texttt{whole_number}} \right) \Rightarrow \underbrace{ \begin{bmatrix} 9 & 4\\ 5 & 6\\ 7 & 8 \end{bmatrix} }_{\textit{hasil}} \]

Menyusun data

Menggunakan SORT(...) dan SORTBY(...).

SORT(...) (1)

  • SORT(...): Fungsi SORT mengurutkan konten rentang atau larik. 1
=SORT(array, [sort_index], [sort_order], [by_col])
  • Nilai default argumen: sort_index <- 1, sort_order <- 1 (Ascending), by_col <- FALSE.

SORT(...) (2)

\[ \texttt{SORT} \left( \underbrace{ \begin{bmatrix} 3 & 2 & 4 & 4\\ 2 & 3 & 1 & 2\\ 4 & 2 & 3 & 2 \end{bmatrix} }_{\texttt{array}} \right) \Rightarrow \underbrace{ \begin{bmatrix} 2 & 3 & 1 & 2\\ 3 & 2 & 4 & 4\\ 4 & 2 & 3 & 2 \end{bmatrix} }_{\textit{hasil}} \]

\[ \texttt{SORT} \left( \underbrace{ \begin{bmatrix} 3 & 2 & 4 & 4\\ 2 & 3 & 1 & 2\\ 4 & 2 & 3 & 2 \end{bmatrix} }_{\texttt{array}} , \underbrace{ 3 }_{\texttt{sort_index}} \right) \Rightarrow \underbrace{ \begin{bmatrix} 2 & 3 & 1 & 2\\ 4 & 2 & 3 & 2\\ 3 & 2 & 4 & 4 \end{bmatrix} }_{\textit{hasil}} \]

SORT(...) (3)

\[ \texttt{SORT} \left( \underbrace{ \begin{bmatrix} 3 & 2 & 4 & 4\\ 2 & 3 & 1 & 2\\ 4 & 2 & 3 & 2 \end{bmatrix} }_{\texttt{array}} , \underbrace{ 3 }_{\texttt{sort_index}} , \underbrace{ -1 }_{\texttt{sort_order}} \right) \Rightarrow \underbrace{ \begin{bmatrix} 3 & 2 & 4 & 4\\ 4 & 2 & 3 & 2\\ 2 & 3 & 1 & 2 \end{bmatrix} }_{\textit{hasil}} \]

\[ \texttt{SORT} \left( \underbrace{ \begin{bmatrix} 3 & 2 & 4 & 4\\ 2 & 3 & 1 & 2\\ 4 & 2 & 3 & 2 \end{bmatrix} }_{\texttt{array}} , \underbrace{ 2 }_{\texttt{sort_index}} , \underbrace{ 1 }_{\texttt{sort_order}} , \underbrace{ \texttt{ TRUE } }_{\texttt{by_col}} \right) \Rightarrow \underbrace{ \begin{bmatrix} 4 & 3 & 4 & 2\\ 1 & 2 & 2 & 3\\ 3 & 4 & 2 & 2 \end{bmatrix} }_{\textit{hasil}} \]

SORTBY(...) (1)

  • SORTBY(...): Fungsi SORTBY mengurutkan konten rentang atau larik berdasarkan nilai dalam rentang atau larik yang terkait. 1
=SORTBY(array, by_array1, [sort_order1], [by_array2], [sort_order2], ...)
  • Nilai default sort_order <- 1 (ascending).
  • Nilai by_array harus berupa vektor atau array 1 dimensi. Dan jenisnya harus sama dengan nilai by_array lainnya (tidak boleh berbeda dimensinya).
  • Jika diurutkan hanya berdasarkan satu array dan berdasarkan kolom/baris di dalam array tersebut, sebaiknya menggunakan SORT.

SORTBY(...) (2)

\[ \mathbf{A} = \begin{bmatrix} \textrm{A} & \textrm{BA} & \textrm{CBBA}\\ \textrm{B} & \textrm{CB} & \textrm{DCCB}\\ \textrm{C} & \textrm{DC} & \textrm{EDDC}\\ \textrm{D} & \textrm{ED} & \textrm{FEED}\\ \textrm{E} & \textrm{FE} & \textrm{GFFE}\\ \textrm{F} & \textrm{GF} & \textrm{IGGF}\\ \textrm{G} & \textrm{IG} & \textrm{AIG} \end{bmatrix}, \mathbf{c}_1 = \begin{bmatrix} 1\\ 3\\ 3\\ 2\\ 2\\ 1\\ 4\\ \end{bmatrix} , \mathbf{c}_2 = \begin{bmatrix} 1\\ 3\\ 5\\ 6\\ 2\\ 7\\ 8\\ \end{bmatrix} \]

\[ \mathbf{r}_1 = \begin{bmatrix} 3 & 1 & 1 \end{bmatrix} , \mathbf{r}_2 = \begin{bmatrix} 7 & 1 & 3 \end{bmatrix} \]

\[ \texttt{SORTBY}( \mathbf{A}, \mathbf{c}_1 ) \lor \texttt{SORTBY}( \mathbf{A}, \mathbf{r}_1, -1, ) \]

\[ \texttt{SORTBY}( \mathbf{A}, \mathbf{c}_1,, \mathbf{c}_2,-1 ) \lor \texttt{SORTBY}( \mathbf{A}, \mathbf{r}_2,-1, \mathbf{r}_1 ) \]

SORTBY(...) (3)

\[ \mathbf{A}, \mathbf{c}_1 \overbrace{\longmapsto}^{ \texttt{SORTBY}( \mathbf{A}, \mathbf{c}_1 ) } \begin{bmatrix} A & BA & CBBA\\ F & GF & IGGF\\ D & ED & FEED\\ E & FE & GFFE\\ B & CB & DCCB\\ C & DC & EDDC\\ G & IG & AIG\\ \end{bmatrix} , \texttt{index} \leftarrow \begin{bmatrix} 1\\ 6\\ 4\\ 5\\ 2\\ 3\\ 7\\ \end{bmatrix} , \texttt{SORT}(\mathbf{c}_1) = \begin{bmatrix} 1\\ 1\\ 2\\ 2\\ 3\\ 3\\ 4\\ \end{bmatrix} \]

SORTBY(...) (4)

\[ \mathbf{A}, \mathbf{c}_1, \mathbf{c}_2 \overbrace{\longmapsto}^{ \texttt{SORTBY}( \mathbf{A}, \mathbf{c}_1,, \mathbf{c}_2, -1 ) } \begin{bmatrix} F & GF & IGGF\\ A & BA & CBBA\\ D & ED & FEED\\ E & FE & GFFE\\ C & DC & EDDC\\ B & CB & DCCB\\ G & IG & AIG\\ \end{bmatrix} , \texttt{index} \leftarrow \begin{bmatrix} 6\\ 1\\ 4\\ 5\\ 3\\ 2\\ 7\\ \end{bmatrix} \]

\[ \texttt{SORT}(\mathbf{c}_1) = \begin{bmatrix} 1\\ 1\\ 2\\ 2\\ 3\\ 3\\ 4\\ \end{bmatrix} , \texttt{SORT}(\mathbf{c}_2, -1) = \begin{bmatrix} 7\\ 1\\ 6\\ 2\\ 5\\ 3\\ 8\\ \end{bmatrix} \]

Mencari data

XLOOKUP(...) (1)

  • XLOOKUP(...): Fungsi XLOOKUP mencari rentang atau array, lalu mengembalikan item yang terkait dengan kecocokan pertama yang ditemukannya. Jika tidak ada kecocokan, XLOOKUP dapat mengembalikan kecocokan terdekat (perkiraan). 1
=XLOOKUP(lookup_value, lookup_array, return_array, [if_not_found], [match_mode], [search_mode])

XMATCH(...) (1)

  • XMATCH(...): Fungsi XMATCH mengembalikan posisi relatif item dalam array atau rentang sel. 1
=XMATCH(lookup_value, lookup_array, [match_mode], [search_mode])

4 Fungsi Baru (2019-2021)

Penggabungan Teks

CONCAT(...) dan TEXTJOIN(...) (1)

  • CONCAT(...): Fungsi CONCAT menggabungkan teks dari beberapa rentang dan/atau string, tetapi tidak menyediakan argumen pemisah atau IgnoreEmpty. 1
=CONCAT(text1, [text2], ...)
  • TEXTJOIN(...): Fungsi TEXTJOIN menggabungkan teks dari beberapa rentang dan/atau string, serta menyertakan pemisah yang Anda tentukan antara tiap nilai teks yang akan digabungkan. Jika pemisah adalah string teks kosong, fungsi ini akan secara efektif menggabungkan rentang. 2
=TEXTJOIN(delimiter, ignore_empty, text1, [text2], ...)

CONCAT(...) dan TEXTJOIN(...) (2)

  • Hal yang membedakan TEXTJOIN(...) dengan CONCAT(...) adalah argumen karakter diantara teks gabungan dengan kondisi ketika sel kosong. Nilai TEXTJOIN(...) === CONCAT(...) ketika argumen delimeter <- "" dan ignore_empty <- TRUE.

\[ \mathbf{T} = \begin{bmatrix} \textrm{nama} & \textrm{saya} & \textrm{taruma}\\ 1 & \textrm{pergi} & 3 \\ \texttt{TRUE} & 100 & \texttt{FALSE}\\ \end{bmatrix} \]

CONCAT(...) dan TEXTJOIN(...) (3)

\[ \mathbf{T} = \begin{bmatrix} \textrm{nama} & \textrm{saya} & \textrm{taruma}\\ 1 & \textrm{pergi} & 3 \\ \texttt{TRUE} & 100 & \texttt{FALSE}\\ \end{bmatrix} \]

\[ \texttt{CONCAT}(\mathbf{T}) = \textrm{namasayataruma1pergi3TRUE100FALSE} \]

\[ \texttt{TEXTJOIN}(\texttt{""}, \texttt{TRUE}, \mathbf{T}) = \textrm{namasayataruma1pergi3TRUE100FALSE} \]

\[ \texttt{TEXTJOIN}(\texttt{" "}, \texttt{TRUE}, \mathbf{T}) = \textrm{nama saya taruma 1 pergi 3 TRUE 100 FALSE} \]

KOLEKSI IF*

IFS(...) dan MINIFS(...)

  • IFS(...): Fungsi IFS memeriksa apakah satu atau beberapa kondisi terpenuhi dan mengembalikan nilai yang sesuai dengan kondisi TRUE pertama. IFS dapat menggantikan beberapa pernyataan IF yang bertumpuk, dan jauh lebih mudah dibaca dengan beberapa kondisi. 1
=IFS(logical_test1, value_if_true1, [logical_test2, value_if_true2], [logical_test3, value_if_true3], ..., value_if_false)
  • MINIFS(...) / MAXIFS(...): Fungsi MINIFS mengembalikan nilai minimal di antara sel yang ditentukan oleh kumpulan persyaratan atau kriteria tertentu / Fungsi MAXIFS mengembalikan nilai maksimal di antara sel yang ditentukan oleh kumpulan persyaratan atau kriteria tertentu. 2 3
=[MIN/MAX]IFS([min/max]_range, criteria_range1, criteria1, [criteria_range2, criteria2], ...)

CONTOH IFS (IF(...))

\[ [-\infty,70) \Rightarrow \text{C}\\ [70,85) \Rightarrow \text{B}\\ [85,\infty) \Rightarrow \text{A} \]

=IF(
  x < 70, "C", 
  IF(
    x < 85, "B",
    "A"
  )
)

CONTOH IFS (IFS(...))

\[ [-\infty,70) \Rightarrow \text{C}\\ [70,85) \Rightarrow \text{B}\\ [85,\infty) \Rightarrow \text{A} \]

=IFS(
  x < 70, "C", 
  x < 85, "B",
  TRUE, "A"
)

SWITCH(...) dan LET(...)

SWITCH(...)

  • SWITCH(...): Fungsi SWITCH mengevaluasi satu nilai (disebut ekspresi) terhadap daftar nilai, dan mengembalikan hasil yang terkait dengan nilai cocok pertama. Jika tidak terdapat kecocokan, nilai default opsional mungkin akan dikembalikan. 1
=SWITCH(expression, value1, result1, [default or value2, result2], ..., [default or value3, result3])

LET(...)

  • LET(...): Fungsi LET menetapkan nama ke hasil perhitungan. Ini memungkinkan menyimpan perhitungan menengah, nilai, atau menetapkan nama di dalam rumus. Nama ini hanya berlaku di dalam lingkup LET fungsi. Mirip dengan variabel dalam pemrograman, LET dilakukan melalui Excel rumus asli Anda. 1
=LET(name1, name_value1, calculation_or_name2, [name_value2, calculation_or_name2], ..., calculation)

CONTOH LET(...) dan SWITCH(...)

\[ \text{A} \Rightarrow 90, \text{B} \Rightarrow 80, \text{C} \Rightarrow 70, \text{D} \Rightarrow 60,\\ \notin \{\text{A}, \text{B}, \text{C}, \text{D}\} \Rightarrow 20 \]

=IFS(
  C$2 = "A", 90,
  C$2 = "B", 80,
  C$2 = "C", 70,
  C$2 = "D", 60,
  TRUE, 20
)

CONTOH LET(...) dan SWITCH(...)

\[ \text{A} \Rightarrow 90, \text{B} \Rightarrow 80, \text{C} \Rightarrow 70, \text{D} \Rightarrow 60,\\ \notin \{\text{A}, \text{B}, \text{C}, \text{D}\} \Rightarrow 20 \]

=LET(
  data, C$2,
  IFS(
    data = "A", 90,
    data = "B", 80,
    data = "C", 70,
    data = "D", 60,
    TRUE, 20
  )
)

CONTOH LET(...) dan SWITCH(...)

\[ \text{A} \Rightarrow 90, \text{B} \Rightarrow 80, \text{C} \Rightarrow 70, \text{D} \Rightarrow 60,\\ \notin \{\text{A}, \text{B}, \text{C}, \text{D}\} \Rightarrow 20 \]

=LET(
  data, C$2,
  SWITCH(
    data,
    "A", 90,
    "B", 80,
    "C", 70,
    "D", 60,
    20
  )
)

Implementasi pada validasi input

Memperbaiki validasi input dari kasus sebelumnya.

Kasus validasi

\[ f : \mathbb{R} \to \mathbb{R} \]

\[ f(\mathbf{x}) = \mathbf{y} = \mathbf{x} + 2 \]

\[ \mathbf{x} \in \mathbb{R}, \mathbf{y} \in \mathbb{R} \]

\[ \mathbf{x} \mapsto \mathbf{x} + 2 \]

\[ \begin{equation} \mathbf{x} \mapsto \texttt{AND} ( \texttt{ISNUMBER}(\mathbf{x}) ) = \begin{cases} \texttt{TRUE} & f : \mathbf{x} \in \mathbb{R} \rightarrow \mathbb{R}\\ \texttt{FALSE} & \textrm{return}\ \texttt{#VALUE!} \\ \texttt{FALSE} & \mathbf{x} \mapsto g(\mathbf{x}) = \texttt{FILTER}(\dots) \mapsto \\ & f: g(\mathbf{x}) \in \mathbb{R} \rightarrow \mathbb{R}\\ \end{cases} \end{equation} \]

  • \(\mathbf{x}\) akan dievaluasi terlebih dahulu dan di filter dengan memilih elemen yang berupa angka saja.
  • \(\mathbf{x} \mapsto \mathbf{y}\) dengan \(y \in \mathbb{R}\) dan \(x \in \mathbb{?}\).

Formula

\[ g : \mathbf{x} \in \mathbb{?} \to \mathbb{R} \]

\[ g(\mathbf{x}) = f( \underbrace{ \texttt{FILTER}(\mathbf{x}, \texttt{ISNUMBER}(\mathbf{x})) }_{\mathbf{y\ \in\ \mathbb{R}}} ) = \underbrace{ f(\mathbf{y}) }_{\in\ \mathbb{R}} = \mathbf{y} + 2 \]

Formula

\[ g(\mathbf{x}) = f( \underbrace{ \texttt{FILTER}(\mathbf{x}, \texttt{ISNUMBER}(\mathbf{x})) }_{\mathbf{y\ \in\ \mathbb{R}}} ) = \underbrace{ f(\mathbf{y}) }_{\in\ \mathbb{R}} = \mathbf{y} + 2 \]

=LET(
  ...
)

Formula

\[ g(\mathbf{x}) = f( \underbrace{ \texttt{FILTER}(\mathbf{x}, \texttt{ISNUMBER}(\mathbf{x})) }_{\mathbf{y\ \in\ \mathbb{R}}} ) = \underbrace{ f(\mathbf{y}) }_{\in\ \mathbb{R}} = \mathbf{y} + 2 \]

=LET(
  x, H8:H15,
  ...
)

Formula

\[ g(\mathbf{x}) = f( \underbrace{ \texttt{FILTER}(\mathbf{x}, \texttt{ISNUMBER}(\mathbf{x})) }_{\mathbf{y\ \in\ \mathbb{R}}} ) = \underbrace{ f(\mathbf{y}) }_{\in\ \mathbb{R}} = \mathbf{y} + 2 \]

=LET(
  x, H8:H15,
  logical_isnumber, ISNUMBER(x),
  ...
)

Formula

\[ g(\mathbf{x}) = f( \underbrace{ \texttt{FILTER}(\mathbf{x}, \texttt{ISNUMBER}(\mathbf{x})) }_{\mathbf{y\ \in\ \mathbb{R}}} ) = \underbrace{ f(\mathbf{y}) }_{\in\ \mathbb{R}} = \mathbf{y} + 2 \]

=LET(
  x, H8:H15,
  logical_isnumber, ISNUMBER(x),
  y, FILTER(x, logical_isnumber),
  ...
)

Formula

\[ g(\mathbf{x}) = f( \underbrace{ \texttt{FILTER}(\mathbf{x}, \texttt{ISNUMBER}(\mathbf{x})) }_{\mathbf{y\ \in\ \mathbb{R}}} ) = \underbrace{ f(\mathbf{y}) }_{\in\ \mathbb{R}} = \mathbf{y} + 2 \]

=LET(
  x, H8:H15,
  y, FILTER(x, ISNUMBER(x)),
  y + 2
)

Formula

\[ g(\mathbf{x}) = f( \underbrace{ \texttt{FILTER}(\mathbf{x}, \texttt{ISNUMBER}(\mathbf{x})) }_{\mathbf{y\ \in\ \mathbb{R}}} ) = \underbrace{ f(\mathbf{y}) }_{\in\ \mathbb{R}} = \mathbf{y} + 2 \]

=LET(
  x, H8:H15,
  y, FILTER(x, ISNUMBER(x)),
  y + 2
)

5 User Defined Lambda (UDL) dengan LAMBDA

LAMBDA dan UDL

  • LAMBDA(...): Gunakan fungsi LAMBDA untuk membuat fungsi kustom yang dapat digunakan kembali dan memanggilnya dengan nama yang mudah dikenali. Fungsi baru tersedia di seluruh buku kerja dan disebut seperti fungsi asli Excel. 1
=LAMBDA(parameter1, [parameter2, parameter3, ...], calculation)
  • User Defined Lambda (UDL) sama halnya dengan User Defined Function (UDF) hanya spesifik pada penggunaan LAMBDA. UDF sendiri adalah fungsi yang dibuat oleh pengguna.

LAMBDA dan LET

  • LAMBDA dan LET biasanya digunakan bersamaan untuk memudahkan pembuatan UDL ataupun membaca/troubleshooting.
  • LAMBDA berfungsi menerima input dan membungkusnya sebagai fungsi baru di Excel sebagai UDL.
  • LET digunakan untuk melakukan perhitungan/kalkulasi setelah menerima input dari LAMBDA.
  • Jika UDL cukup sederhana, LET tidak perlu digunakan.

Sintaks LAMBDA dan LET

=LAMBDA(parameter1, [parameter2, parameter3, ...], calculation)
  • Untuk memudahkan membaca kode, buat baris baru diantara (...).

Sintaks LAMBDA dan LET

=LAMBDA(
  parameter1, 
  [parameter2, parameter3, ...],
  calculation
)
  • Ubah calculation dengan LET(...).

Sintaks LAMBDA dan LET

=LAMBDA(
  parameter1, 
  [parameter2, parameter3, ...],
  LET(
    name1, value1,
    [name2, value2, name3, value3, ...],
    calculation
  )
)
  • Argumen parameter yang berasal dari LAMBDA, dapat langsung digunakan di LET tanpa melakukan pendefinisian ulang.

Sintaks LAMBDA dan LET

=LAMBDA(
  parameter1, 
  parameter2,
  parameter3,
  LET(
    name1, parameter1 + parameter2,
    name2, parameter3 - name1
    name1 / parameter2
  )
)
  • parameter2 bisa langsung digunakan pada LET tanpa pendefinisian ulang.

Contoh Kasus

Mengurangi setiap elemen pada vektor dengan setengah rata-ratanya.

Deskripsi Kasus

  • Mengurangi setiap elemen dari numeric vector (\(\mathbf{x}\)) dengan setengah dari rata-ratanya (\(\frac{\texttt{mean}(\mathbf{x})}{2}\)).

\[ f : \mathbf{x} \in \mathbb{R} \to \mathbb{R} \]

\[ f(\mathbf{x}) = \mathbf{x} - \frac{\overline{\mathbf{x}}}{2} = \mathbf{x} - \frac{\texttt{AVERAGE}(\mathbf{x})}{2} \]

Fungsi LAMBDA

\[ f(\mathbf{x}) = \mathbf{x} - \frac{\texttt{AVERAGE}(\mathbf{x})}{2} \]

=LAMBDA(
  parameter1, 
  [parameter2, parameter3, ...],
  calculation
)
  • menentukan input variabel untuk fungsi LAMBDA.
  • \(f(\mathbf{x})\) menunjukkan input fungsi \(f\) hanya vektor \(\mathbf{x}\)

input LAMBDA

\[ f(\mathbf{x}) = \mathbf{x} - \frac{\texttt{AVERAGE}(\mathbf{x})}{2} \]

=LAMBDA(
  vector,
  calculation
)
  • Karena fungsi \(f\) memiliki perhitungan AVERAGE(...), yang sebaiknya disimpan di variabel sementara, maka diperlukan kalkulasi menggunakan LET(...).

Menggunakan LET

\[ f(\mathbf{x}) = \mathbf{x} - \frac{\texttt{AVERAGE}(\mathbf{x})}{2} \]

=LAMBDA(
  vector,
  LET(
    name1, value1,
    [name2, value2, name3, value3, ...],
    calculation
  )
)
  • Karena pada persamaan asli \(f\) menggunakan simbol \(\mathbf{x}\), bisa dilakukan assignment / pendefinisian berupa x <- vector.

Argumen redundant / berulang

\[ f(\mathbf{x}) = \mathbf{x} - \frac{\texttt{AVERAGE}(\mathbf{x})}{2} \]

=LAMBDA(
  vector,
  LET(
    x, vector,
    ..., ...,
    calculation
  )
)
  • x <- vector merupakan argumen yang tidak perlu (redundant / berulang) dikarenakan tidak ada modifikasi pada input vector.
  • Selain itu, pada proses pengembangan LAMBDA lebih baik menggunakan nama variabel yang mudah diingat atau dipahami.

Perhitungan dalam fungsi LET

\[ f(\mathbf{x}) = \mathbf{x} - \frac{\texttt{AVERAGE}(\mathbf{x})}{2} \]

=LAMBDA(
  vector,
  LET(
    ..., ...,
    calculation
  )
)
  • Nilai rata-rata bisa disimpan sebagai variabel avg.
avg <- AVERAGE(vector)
  • Variabel halfavg menyatakan nilai setengah dari rata-rata vektor.
halfavg <- avg / 2
  • Hasil akhir dapat disimpan sebagai variabel result.
result <- vector - halfavg

Mengisi hasil dari LAMBDA

\[ f(\mathbf{x}) = \mathbf{x} - \frac{\texttt{AVERAGE}(\mathbf{x})}{2} \]

=LAMBDA(
  vector,
  LET(
    avg, AVERAGE(vector),
    halfavg, avg / 2,
    result, vector - halfavg,
    ...
  )
)
  • Fungsi LAMBDA ini masih belum mengeluarkan hasil atau return dari fungsinya.
  • Pada argumen terakhir LET disampaikan kembali hasil yang diperoleh dari seluruh perhitungan. Yaitu result.

Menghindari pendefinisian berulang

\[ f(\mathbf{x}) = \mathbf{x} - \frac{\texttt{AVERAGE}(\mathbf{x})}{2} \]

=LAMBDA(
  vector,
  LET(
    avg, AVERAGE(vector),
    halfavg, avg / 2,
    result, vector - halfavg,
    result
  )
)
  • Pada baris ke-6 dan ke-7 bisa dibuat lebih sederhana menjadi satu baris dan langsung memberikan return atau hasil dari fungsi LAMBDA.

Formula akhir

\[ f(\mathbf{x}) = \mathbf{x} - \frac{\texttt{AVERAGE}(\mathbf{x})}{2} \]

=LAMBDA(
  vector,
  LET(
    avg, AVERAGE(vector),
    halfavg, avg / 2,
    vector - halfavg
  )
)
  • Fungsi LAMBDA sudah lengkap dan bisa langsung digunakan.

Rekap

\[ f : \mathbf{x} \in \mathbb{R} \to \mathbb{R} \]

\[ f(\mathbf{x}) = \mathbf{x} - \frac{\texttt{AVERAGE}(\mathbf{x})}{2} \]

=LAMBDA(
  vector,
  LET(
    avg, AVERAGE(vector),
    halfavg, avg / 2,
    vector - halfavg
  )
)

Menggunakan formula di Excel (1)

\[ f : \mathbf{x} \in \mathbb{R} \to \mathbb{R} \]

\[ f(\mathbf{x}) = \mathbf{x} - \frac{\texttt{AVERAGE}(\mathbf{x})}{2} \]

=LAMBDA(
  vector,
  LET(
    avg, AVERAGE(vector),
    halfavg, avg / 2,
    vector - halfavg
  )
)
  • Salin formula diatas dan simpan sebagai fungsi bernama HALFAVG(...).

Menggunakan formula di Excel (2)

Pengembangan lebih lanjut

Validasi input (1)

\[ g : \mathbf{y} \in \mathbb{?} \to \mathbb{R} \]

\[ \mathbb{y}_{\textit{filtered}} \leftarrow \text{VALIDASI}(\mathbf{y}) \]

\[ g(\mathbf{y}) = \mathbf{y}_{\textit{filtered}} - \frac{\texttt{AVERAGE}(\mathbf{y}_{\textit{filtered}})}{2} \]

=LAMBDA(
  vector,
  LET(
    ...,...,
    avg, AVERAGE(vector),
    halfavg, avg / 2,
    vector - halfavg
  )
)

Validasi input (2)

\[ g(\mathbf{y}) = \mathbf{y}_{\textit{filtered}} - \frac{\texttt{AVERAGE}(\mathbf{y}_{\textit{filtered}})}{2} \]

=LAMBDA(
  vector,
  LET(
    vector_filtered, FILTER(vector, ISNUMBER(vector)),
    avg, AVERAGE(vector_filtered),
    halfavg, avg / 2,
    vector_filtered - halfavg
  )
)

Refactoring (1)

\[ g(\mathbf{y}) = \mathbf{y}_{\textit{filtered}} - \frac{\texttt{AVERAGE}(\mathbf{y}_{\textit{filtered}})}{2} \]

=LAMBDA(
  vector,
  LET(
    vector_filtered, FILTER(vector, ISNUMBER(vector)),
    avg, AVERAGE(vector_filtered),
    halfavg, avg / 2,
    vector_filtered - halfavg
  )
)
  • Refactoring merupakan perubahan dari kode program yang sudah ada tanpa mengubah hasil dari program tersebut.
  • variabel avg bisa langsung diterapkan pada variabel halfavg.

Refactoring (2)

\[ g(\mathbf{y}) = \mathbf{y}_{\textit{filtered}} - \frac{\texttt{AVERAGE}(\mathbf{y}_{\textit{filtered}})}{2} \]

=LAMBDA(
  vector,
  LET(
    vector_filtered, FILTER(vector, ISNUMBER(vector)),
    halfavg, AVERAGE(vector_filtered) / 2,
    vector_filtered - halfavg
  )
)

Optional argument (1)

\[ g(\mathbf{y}) = \mathbf{y}_{\textit{filtered}} - \frac{\texttt{AVERAGE}(\mathbf{y}_{\textit{filtered}})}{2} \]

\[ \mathbf{y}, n \mapsto g(\mathbf{y}, n) = \mathbf{y}_{\textit{filtered}} - \frac{\texttt{AVERAGE}(\mathbf{y}_{\textit{filtered}})}{n} \]

\[ \begin{equation} n = \begin{cases} \dots & \mathbf{y}, n = 2 \mapsto g(\mathbf{y}, 2) = f(\mathbf{y}_{\textit{filtered}})\\ n & \mathbf{y}, n \mapsto g(\mathbf{y}, n) \end{cases} \end{equation} \]

Optional argument (2)

\[ \mathbf{y}, n \mapsto g(\mathbf{y}, n) = \mathbf{y}_{\textit{filtered}} - \frac{\texttt{AVERAGE}(\mathbf{y}_{\textit{filtered}})}{n} \]

=LAMBDA(
  vector,
  LET(
    vector_filtered, FILTER(vector, ISNUMBER(vector)),
    halfavg, AVERAGE(vector_filtered) / 2,
    vector_filtered - halfavg
  )
)

Optional argument (3)

\[ \mathbf{y}, n \mapsto g(\mathbf{y}, n) = \mathbf{y}_{\textit{filtered}} - \frac{\texttt{AVERAGE}(\mathbf{y}_{\textit{filtered}})}{n} \]

=LAMBDA(
  vector,
  ...,
  LET(
    ...,...,
    vector_filtered, FILTER(vector, ISNUMBER(vector)),
    halfavg, AVERAGE(vector_filtered) / 2,
    vector_filtered - halfavg
  )
)

Optional argument (4)

\[ \mathbf{y}, n \mapsto g(\mathbf{y}, n) = \mathbf{y}_{\textit{filtered}} - \frac{\texttt{AVERAGE}(\mathbf{y}_{\textit{filtered}})}{n} \]

=LAMBDA(
  vector,
  [n],
  LET(
    ...,...,
    vector_filtered, FILTER(vector, ISNUMBER(vector)),
    halfavg, AVERAGE(vector_filtered) / n,
    vector_filtered - halfavg
  )
)

Optional argument (5)

\[ \mathbf{y}, n \mapsto g(\mathbf{y}, n) = \mathbf{y}_{\textit{filtered}} - \frac{\texttt{AVERAGE}(\mathbf{y}_{\textit{filtered}})}{n} \]

=LAMBDA(
  vector,
  [n],
  LET(
    n, IF(ISOMITTED(n), 2, n),
    vector_filtered, FILTER(vector, ISNUMBER(vector)),
    halfavg, AVERAGE(vector_filtered) / n,
    vector_filtered - halfavg
  )
)

\[ \begin{equation} n \mapsto \texttt{ISOMITTED}(n) = \begin{cases} \texttt{TRUE} & n \leftarrow 2 \\ \texttt{FALSE} & n \leftarrow n \end{cases} \end{equation} \]

Formula Akhir

\[ \mathbf{y}, n \mapsto g(\mathbf{y}, n) = \mathbf{y}_{\textit{filtered}} - \frac{\texttt{AVERAGE}(\mathbf{y}_{\textit{filtered}})}{n} \]

=LAMBDA(
  vector,
  [n],
  LET(
    n, IF(ISOMITTED(n), 2, n),
    vector_filtered, FILTER(vector, ISNUMBER(vector)),
    halfavg, AVERAGE(vector_filtered) / n,
    vector_filtered - halfavg
  )
)
  • Formula tersebut disimpan sebagai HALFAVGN di Formulas Name Manager.
  • Sintaksnya =HALFAVGN(vector, [n]).
  • =HALFAVGN(D5:D10) (maka \(n=2\)).
  • =HALFAVGN(D5#, 4) (maka \(n=4\)).

feidlambda III

Pengenalan mengembangkan LAMBDA dan fungsi yang berkaitan dengan LAMBDA

Pengenalan Advanced Formula Environment (AFE)

  • Excel add-ins yang memudahkan mengatur kumpulan formula pada lembar kerja.
  • Alternatif Formulas Name Manager.
  • Memiliki fitur syntax highlighting dan shortcut umum untuk coding.
  • Dapat import UDL hasil dari orang lain menggunakan GitHub Gist.

Demonstrasi menggunakan AFE (1)

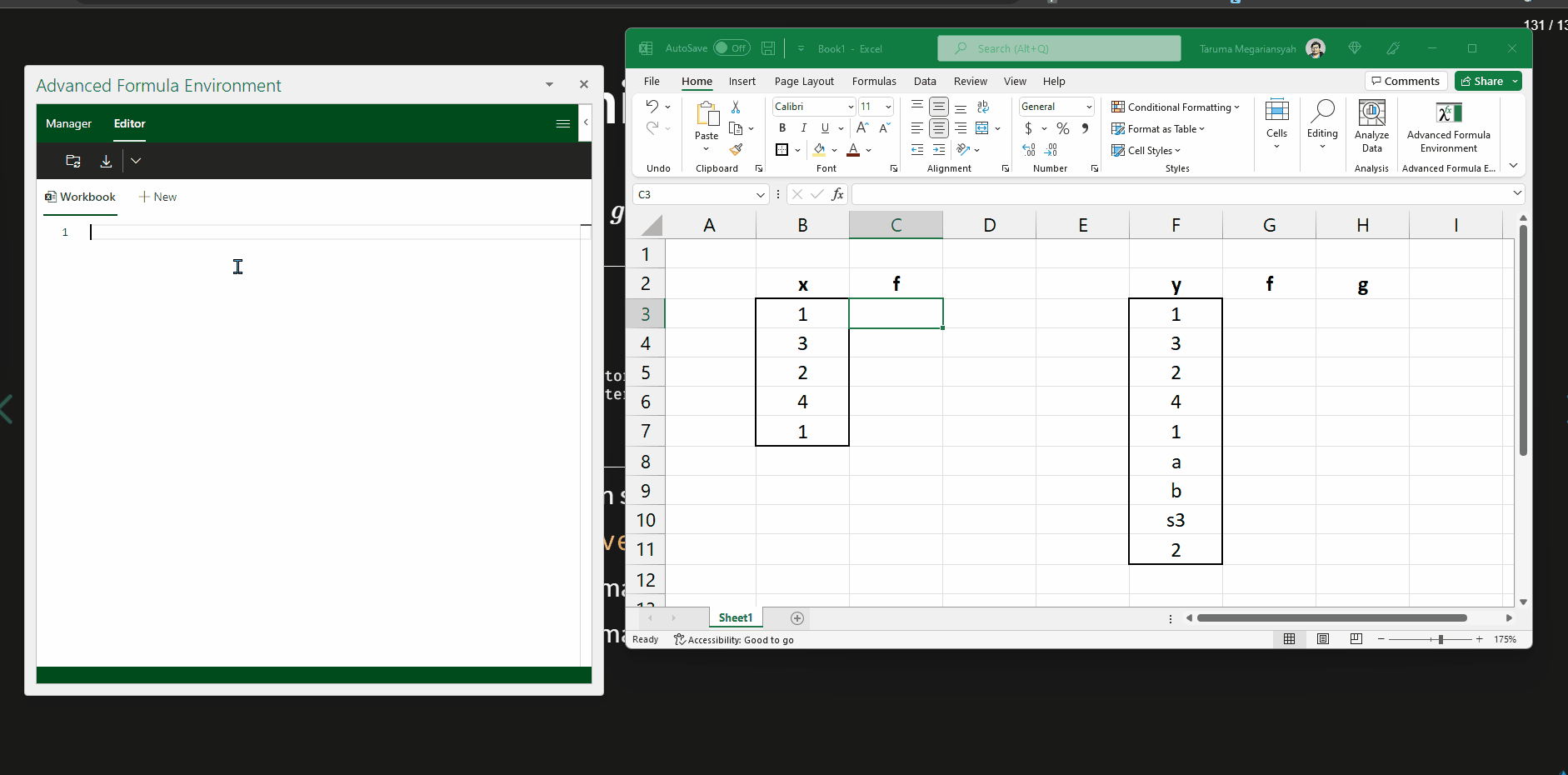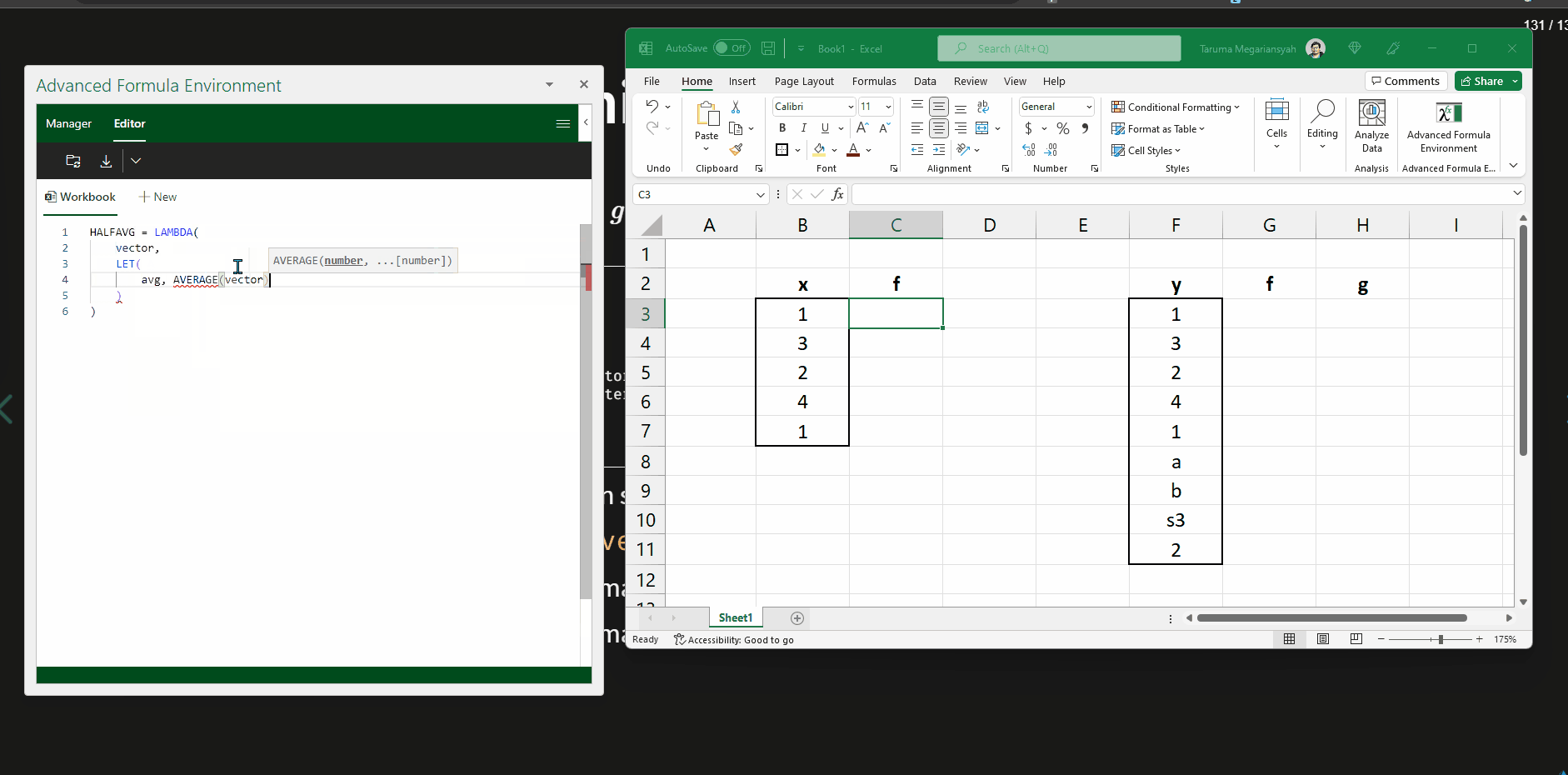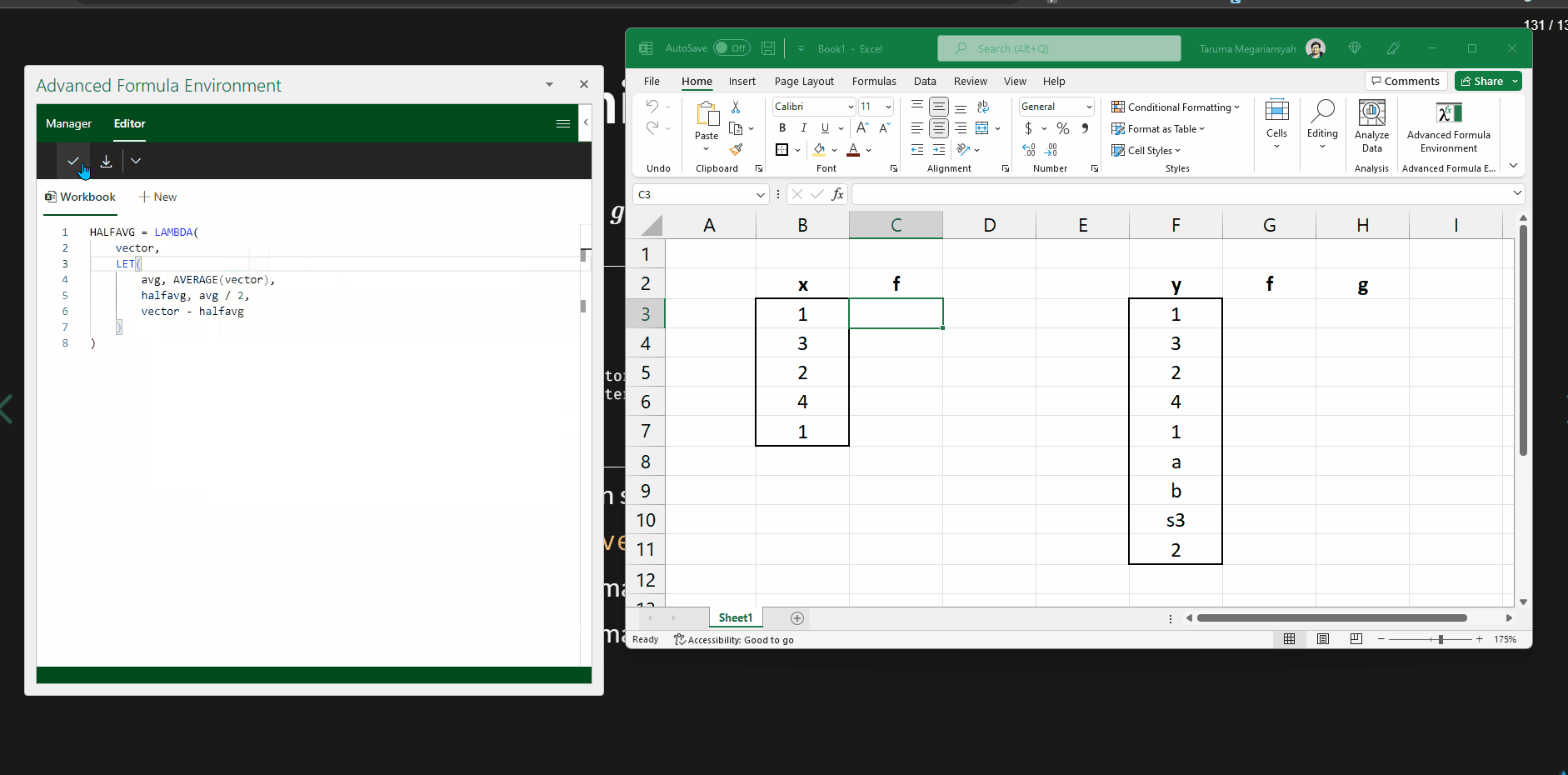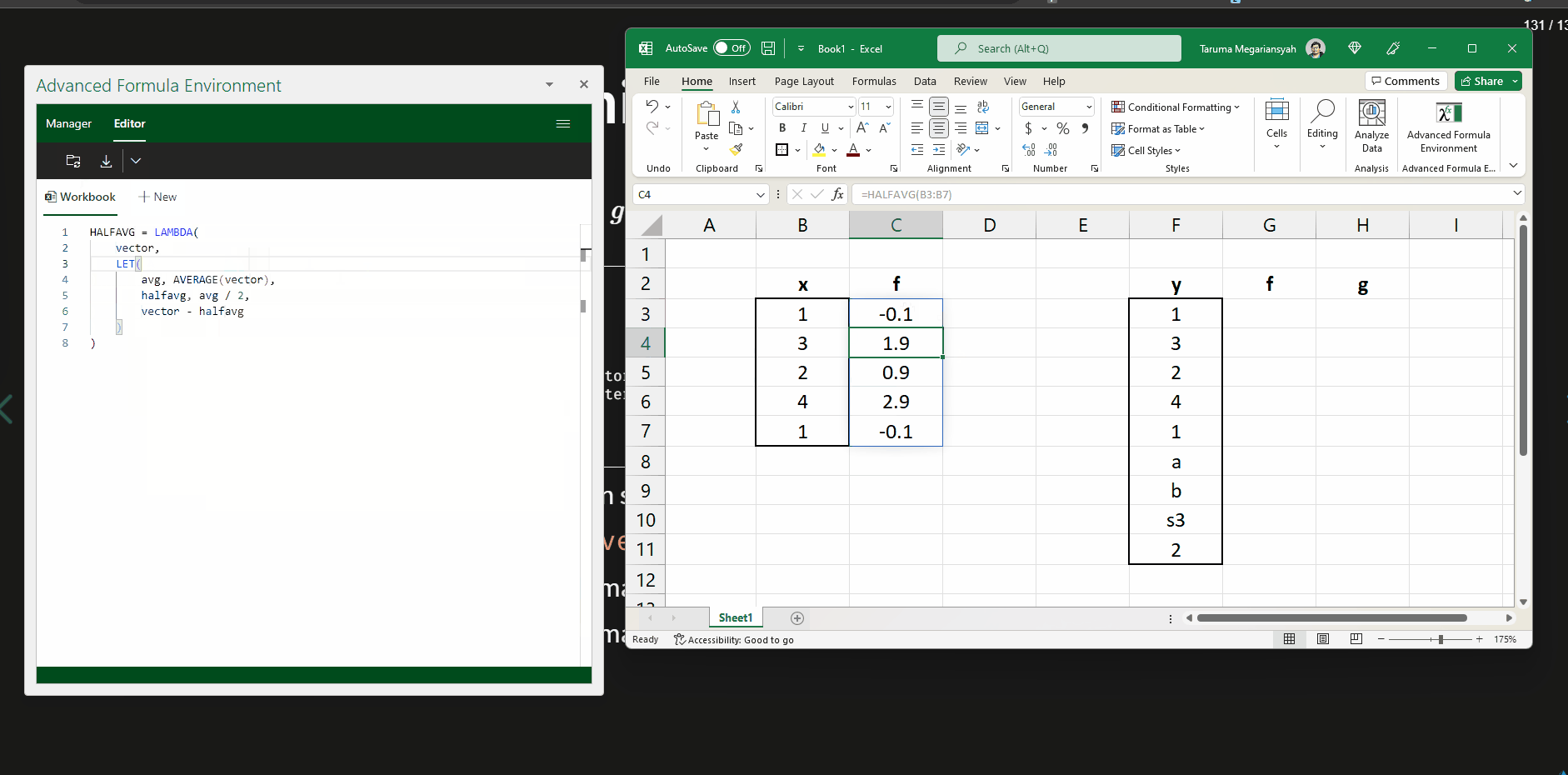
Demonstrasi menggunakan AFE (1)

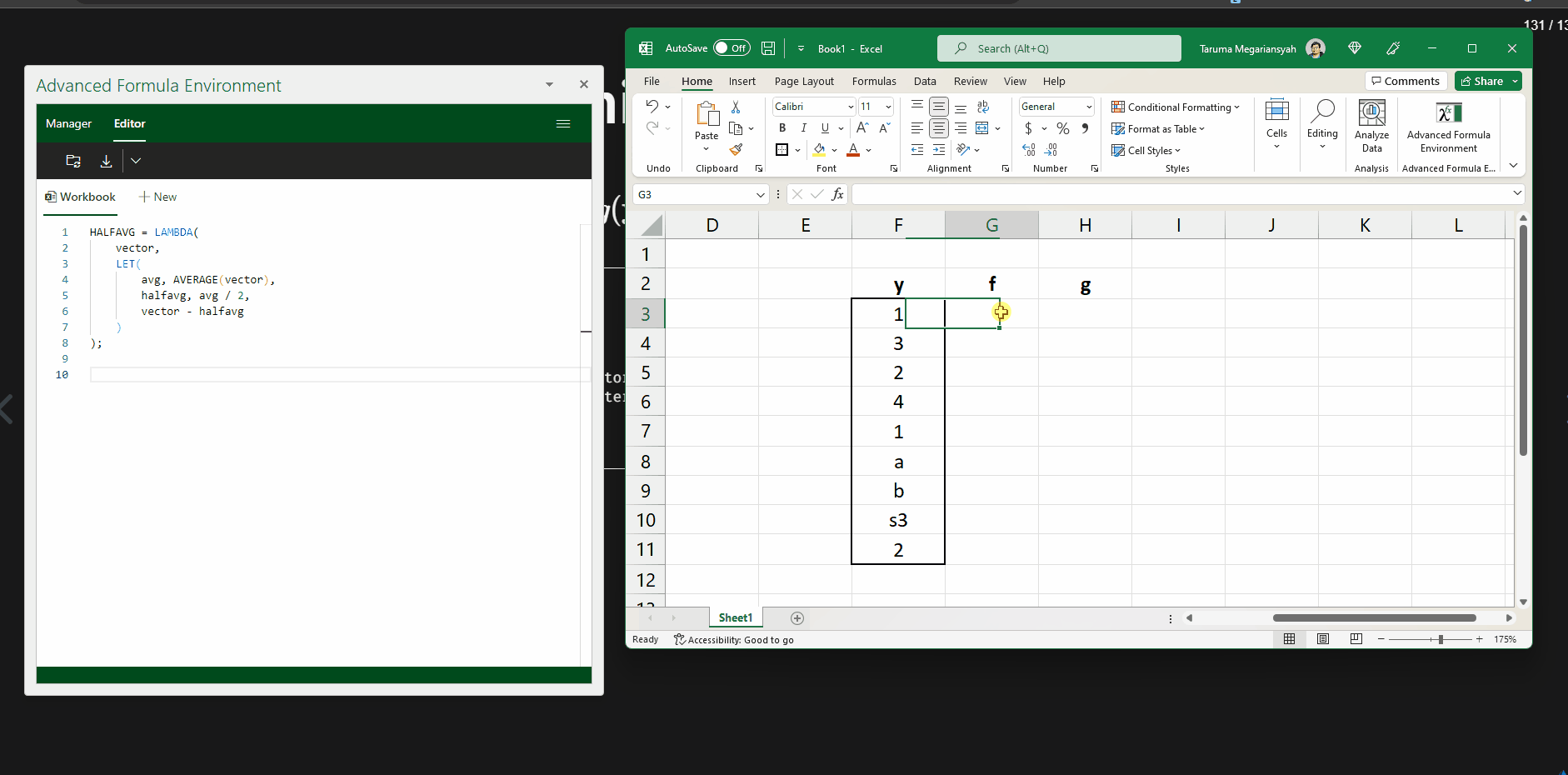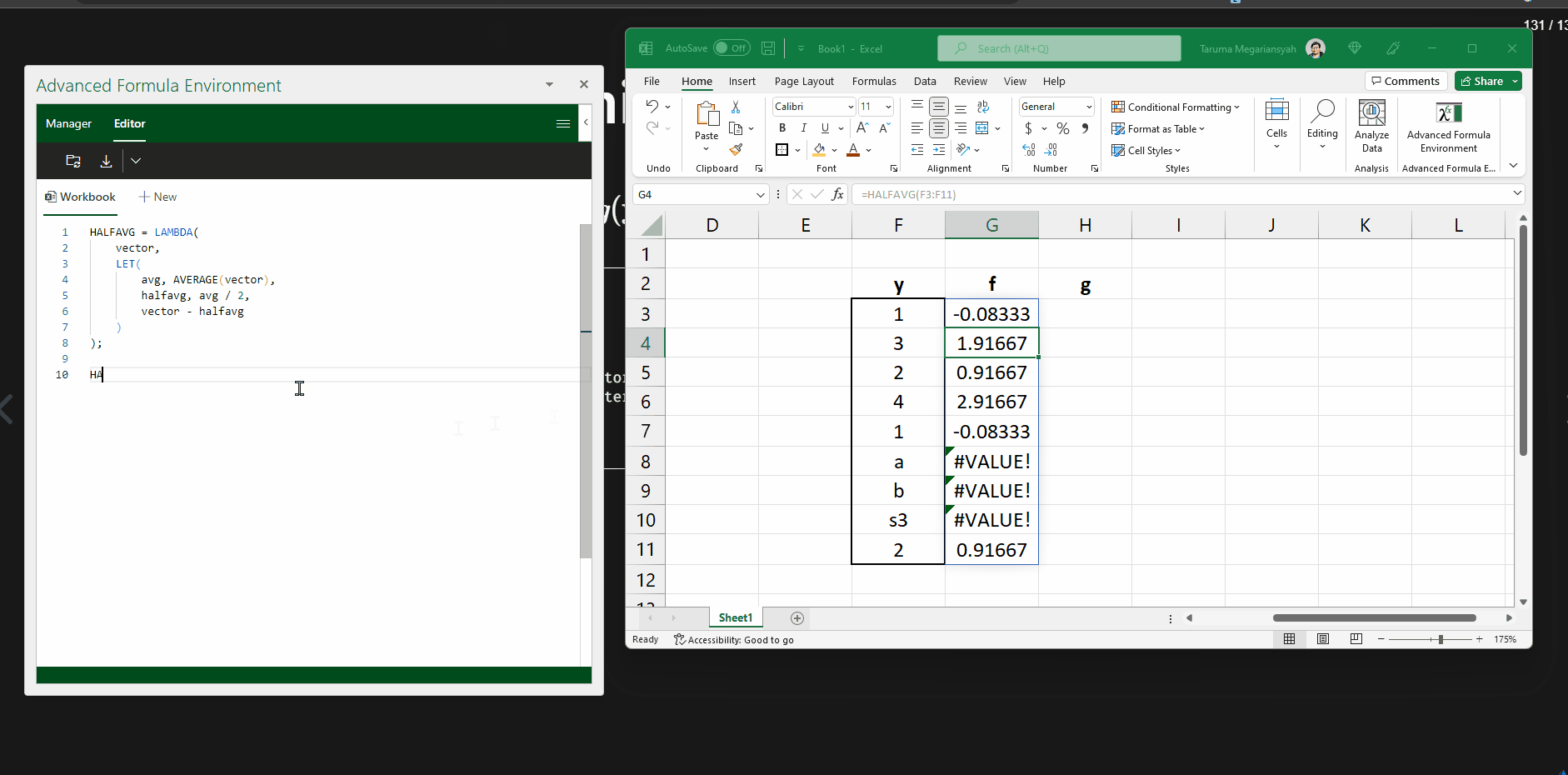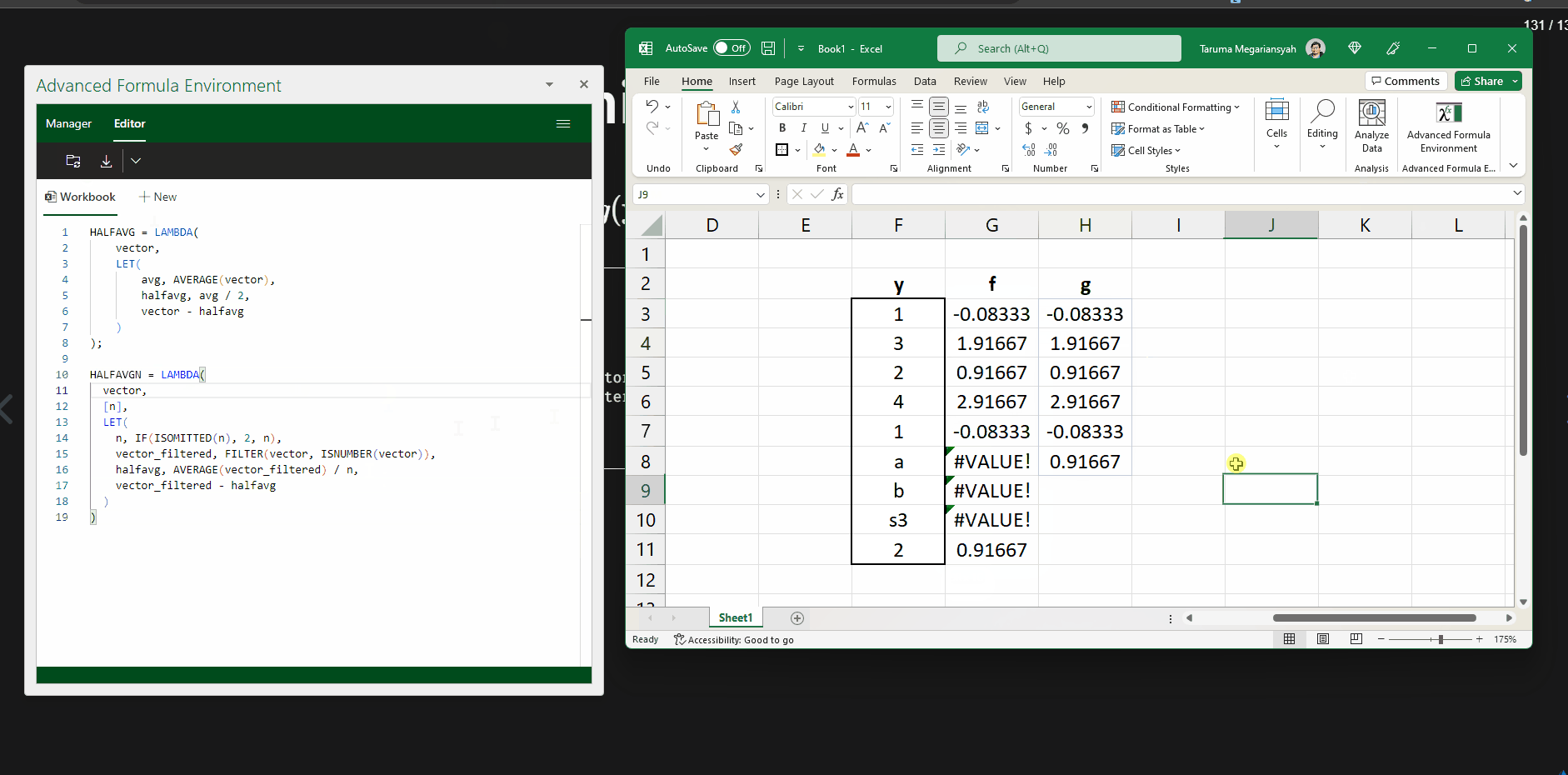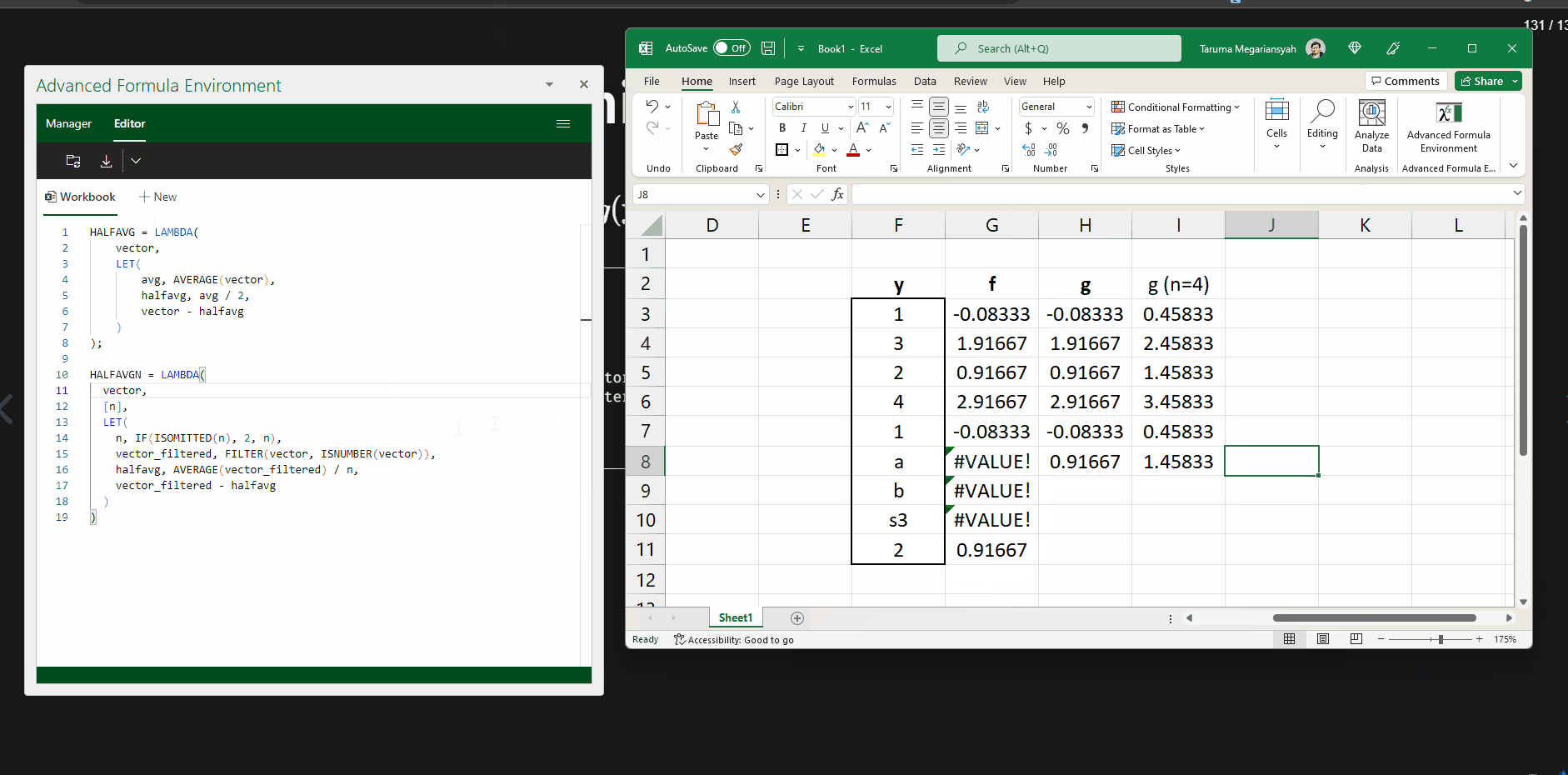
Daftar fungsi yang dibahas di feidlambda III

  • Fungsi vektorisasi SCAN, MAP, REDUCE.
  • Transformasi kolom dengan TOCOL, TOROW, WRAPCOLS, WRAPROWS.
  • Menggabungkan array dengan VSTACK dan HSTACK
  • Manipulasi array dengan DROP, EXPAND.
  • Memilih kolom/baris dengan CHOOSECOLS dan CHOOSEROWS, TAKE
  • Fungsi teks TEXTAFTER, TEXTBEFORE, TEXTSPLIT, VALUETOTEXT, ARRAYTOTEXT.
  • Iterasi dengan BYCOL dan BYROW,

Terima Kasih

Taruma Sakti Megariansyah, hi@taruma.info

Lanjut ke Latihan >

Edit this presentation | Report an issue